1. 32 × 34 = 32+4 = 36
The bases are the same (both 3's), so the exponents are added.
(3×3)×(3×3×3×3)=(3×3×3×3×3×3) |
2. 22(23) (25) = 22+3+5 = 210
The bases are the same (all 2's), so the exponents are added.
(2×2)×(2×2×2)×(2×2×2×2×2) = 210
|
3. 32 + 34 ≠ 32+4
Oops!! This problem is NOT multiplication. This rule does not apply to addition.
Remember, this rule applies only when multipling the terms.
|
4. (-2)3 • 125 • (-2)6 • 12 = (-2)9 • 126
Be sure to only add the exponents for the bases that are the same. Also, do not forget that 12 has an exponent of 1 that is implied, but not written.
(-2×-2×-2)×(-2×-2×-2×-2×-2×-2) = (-2)9
(12×12×12×12×12)×(12) = 126
|
5. 92 × 24 = ?
This multiplication rule cannot be applied to this problem since the bases are not the same. In some such cases, as you will see in Example 7, it may be possible to rewrite one of the terms in the same base as the other term, but that is not the case here.
|
6. 83 × 25 = 29 × 25 = 214
Sneaky one!!! In this problem 8 can be written as 2 cubed, thus creating the same base for both terms.. 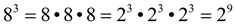 . You get to apply the Rule twice in this one problem. . You get to apply the Rule twice in this one problem.
|
7. 64 × 36 = 64 × 62 = 66
The 36 can be written as a power of 6 making the bases the same value. The needed CHANGE was easier to see in this problem, than in Example 7.
|
8. x3 • x5 • x6 = x3+5+6 = x14
Now, let's see what happens with variables. The bases are the same (all x's), so the exponents are added. |
9. 5a2 • 2a3 • a4 = 5 • 2 • 1 • a2+3+4
= 10a9
If there terms being multiplied have numbers in front of the variables (coefficients), those numbers are multiplied times on another.
The bases are the same (all a's), so the exponents are added. The numbers in front of the bases (5, 2, and 1) are multiplied. |
10. 3x2 (2x3 + 4) = 3x2 (2x3) + 3x2 (4)
= 6x5 + 12x2
The distributive property is applied in this problem. (Multiply each term inside the parentheses by the 3x2 term.)
Then the exponents in the first portion are added since their bases are the same. The numbers in front (the coefficients) are multiplied.
Remember that you cannot add 6x5 and 12x2 since they are not similar (like) terms.
|