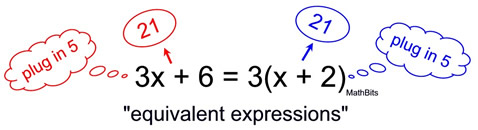|
"Expressions" that represent the same value may appear in several different forms,
referred to as equivalent expressions.
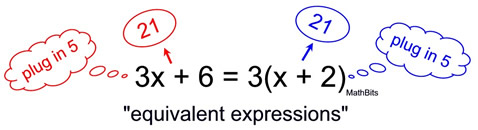
The Distributive Property ensures that 3x + 6 and 3(x + 2) are equivalent expressions.
To double check, we substituted the number 5 into each expression and got the result 21 from both.
You can show that expressions are equivalent:
| • algebraically: |
|
• numerically: |
by showing, through algebraic computations, that both expressions can be represented as the same expression.
- remove parentheses
- combine similar terms
- arrange terms from both
expressions in the same order
- keep working until both
expressions are exactly the same |
|
by showing, through numerical substitution, that the same number(s) replacing the variable(s) in both expressions yield the same numeric results.
- substitute the same number(s) for each
variable in each expression
- compute the numerical results of each expression
- the numerical results will be the same for both expressions
NOTE: Avoid choosing the number 0 for substituting. |
|
When determining equivalent expressions:
take your time and LOOK CAREFULLY!
Some expressions may not LOOK equivalent at first glance,
but upon further examination will be equivalent.
|
The number 3 will be used for the numerical checks in the following examples.
|
Are these expressions equivalent?
7x + 2x and 14x
|
Numerical check (x = 3)
7(3) + 2(3) = 27
14(3) = 42
27
≠ 42 |
Algebraic check:
7x + 2x = 9x
9x ≠ 14x |
Not Equivalent!

|

|
Are these expressions equivalent?
5(x - 2) and 5x - 10
|
Numerical check (x = 3)
5(3 - 2) = 5
5(3) - 10 = 5
CHECK |
Algebraic check:
5(x - 2) = 5x - 10
Distributive Property
CHECK |
Equivalent!

|
In this example, by the Distributive Property 5(x - 2) = 5(x) - 5(2) = 5x - 10.
|

|
Are these expressions equivalent?
6(3x) and 9x
|
Numerical check ( x = 3)
6(3(3)) = 54
9(3) = 27
54
≠ 27 |
Algebraic check:
6(3x) = 18x
9x
≠ 18x
|
Not Equivalent!

|

 |
Show, by completing the table, whether the given expressions are equivalent to
6(x + 2).
Use x = 3 for numerical checking.
|
The distributive property shows 6(x + 2) = 6x + 12. And when x = 3, 6(3 + 2) = 6(5) = 30
Expression |
Y/N |
Numerical Check
(Let x = 3) |
Algebraic Check |
a) 6x + 2 |
NO |
6(3) + 2 = 20 ≠ 30 |
6x + 2 ≠ 6(x + 2) = 6x + 12
|
b) 3x + 6 + 3x + 6 |
YES |
3(3) + 6 + 3(3) + 6 = 30 |
3x + 6 + 3x + 6 = 6x + 12
|
c) 6x + 12 |
YES |
6(3) + 12 = 30 |
6x + 12 = 6(x + 2) = 6x + 12
|
d) 3(x + 2) + 3(x + 2) |
YES |
3(3 + 2) + 3(3 + 2) = 30 |
3(x + 2) + 3(x + 2) =
3x + 6 + 3x + 6 = 6x + 12
|
e) 3(x + 2) + 3x |
NO |
3(3 + 2) + 3(3) =
24 ≠ 30 |
3(x + 2) + 3x = 3x + 6 + 3x
= 6x + 6 ≠ 6x + 12
|

|
Are these expressions equivalent?
18x + 27 = 9(2x + 3)
|
Numerical check ( x = 3)
18(3) + 27 = 81
3(6(3)+9) = 81
CHECK |
Algebraic check:
18x +27 = 9(2x +3)
18x + 27 = 18x + 27
Distributive Property applied
to the right hand side.
CHECK
|
Equivalent!

|
In this example, we could also use the Distributive Property in reverse.
Start with 18x + 27.
Factor out the GCF of 9.
And we get 9(2x + 3). CHECK.
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|