When two (or more) integers are multiplied together, the answer is called a product.
The integers that were multiplied together are called the factors of the product.

3 • 6 = 18 (3 and 6 are factors of 18)

A number can have a list of factors. Factors of 18 are 1, 2, 3, 6, 9, and 18.
Any number that divides into 18 without a remainder is one of the factors of 18.
Remember: If you are dealing with a prime number, the only factors will be the number itself and one.

Listing Factors to find common factors:
One method of finding common factors is by "listing" the factors of each number and seeing what factors they have in "common" (they share).

 The greatest common factor (GCF) of two (or more) integers is the largest integer
that divides exactly into both (or all) numbers.
It is the largest integer that is a factor of both (or all) numbers.
It is the largest of the common factors.
Note: GCF is sometimes referred to as HCF (highest common factor).

Listing Factors to find GCF:

Consider the numbers 18, 24, and 36. Their factors are: Factors of 18: 1, 2, 3, 6, 9, 18 Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24 Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36 Their common factors are 1, 2, 3, and 6. Their greatest common factor is 6. (6 is the largest integer that will divide evenly into all three numbers)

Using Prime Factorization to find GCF:
Another method of finding common factors is to apply "prime factorization" to both numbers and observe the shared (common) factors.

Circle the factors that are shared among the three numbers.
Even if there are multiple values that are the same, only circle one of each value at a time with its match in the other numbers. Don't worry about "left overs".
Multiply these circled values together (within each number) to find the greatest common factor.
All of these numbers share a factor of 6, which is also their greatest common factor.

Using Prime Factorization to find GCF of Large Numbers:

Another method of finding the greatest common factor is by using prime factorization.
This method is particularly useful when the numbers are LARGE
and "listing" the factors becomes too time consuming.

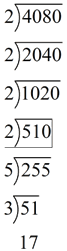
What is the greatest common factor of 4080 and 1920? Listing the factors of these numbers would be too tedious. Instead, let's find the prime factorizations of these numbers. 4080   1920 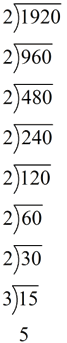4080 = 2 x 2 x 2 x 2 x 5 x 3 x 17 = 24 x 5 x 3 x 17 1920 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 5 = 27 x 3 x 5 Shared (in common): 2 x 2 x 2 x 2 x 3 x 5 = 240 The greatest common factor is 240.

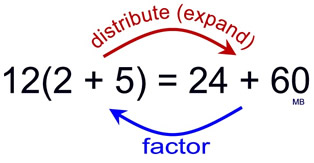
The Distributive Property and the GCF

The distributive property, along with the greatest common factor, can be used to rewrite a "factored" sum of two or more numbers.

Distributive Property: a (b + c) = a • b + a • c

Example: Rewrite 35 + 42. Step 1: Find the GCF of both numbers.      Factors of 35: 1, 5, 7, 35      Factors of 42: 1, 2, 3, 6, 7, 14, 21, 35      The GCF is 7. Step 2: Write the sum, 35 + 42 as 7( __ + __ ).      The blanks are filled in with 35 ÷ 7 = 5 and 42 ÷ 7 = 6. Step 3: Write the final answer:      35 + 42 = 7 ( 5 + 6) where 7 is the GCF, greatest common factor for 35 and 42. And 5 and 6 have no common factors.

See Example 4 under Factoring - Numerical Examples for more on this topic.

36 + 81 = 9(4 + 9) where 9 is the GCF of 36 and 81.

75 + 100 = 25(3 + 4) where 25 is the GCF of 75 and 100.

In these examples, the distributive property is being used to rewrite the sum of two positive integers having a common factor, such as (36 + 81), as their GCF times the sum of two positive integers with no common factors, such as 9(4 + 9).

This type of factoring is using the distributive property in reverse.

Common factors can be used when reducing or simplifying fractions.

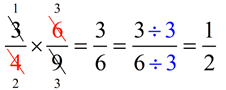
The common factor of 3 and 9 (which is 3) was used to reduce a portion of the problem. The common factor of 4 and 6 (which is 2) was used to reduce another portion of the problem.
The common factor of 3 and 6 (which is 3) was used to arrive at the simplest form of the answer.

The least common multiple (LCM) is the smallest number into which
two (or more) integers will divide exactly.
It is the smallest number containing all factors of both numbers.

When looking for a LCM, list the multiples of each of the numbers.
(That is, multiply the number x2, x3, x4, x5, ...)
Keep the lists going for both numbers until a common (shared) number from each list appears.

There are a lot of common multiples, but only one least common multiple:
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27 30 33, 36, 39, 42, 45, ...
Multiples of 7: 7, 14, 21, 28, 35, 42, 29, ...
Notice that 42 is also a common multiple of 3 and 7 (and there are many others).
But the "least" (the smallest) common multiple is 21.

As we saw in the "greatest common factor" example above, "listing" works nicely as long as the numbers are relatively small. The same is true for finding the "least common multiple".
In the previous example, we used prime factorization to obtain:

4080 = 2 x 2 x 2 x 2 x 5 x 3 x 17 = 2⁴ x 5 x 3 x 17

1920 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 5 = 2⁷ x 3 x 5

Now, the least common multiple will contain all factors of both numbers.
The LCM is 2⁷ x 3 x 5 x 17 = 32,640
(The factor of 2⁴ is already covered within 2⁷.)

The least common multiple is being used when finding a common denominator for working with fractions. When adding the fractions in the problem below, the least common multiple of 6 and 4 is 12, making 12 the least common denominator.

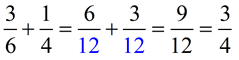
The common factor of 3 (for 9 and 12) was used to reduce the fraction to its simplest form.

The GCF and LCM can be observed using Prime Factor Diagrams.
These are Venn Diagrams containing prime factors.

Find the GCF and LCM for 24 and 30.

The GCF is the product of the prime factors that overlap.
The LCM is the product of all of the prime factors observed in the diagram.

For help with LCM and GCF on your calculator, click here.