|
The features of a function graph can show us many aspects of the relationship represented by the function. Let's take a look at the more popular graphical features.
 Intercepts are the locations (points) where the graph crosses (or touches) either the x-axis or y-axis.
Intercepts are the locations (points) where the graph crosses (or touches) either the x-axis or y-axis.
 To find the y-intercept, look where x = 0. To find the y-intercept, look where x = 0.
Remember: the
y-intercept will have an x-coordinate of 0.
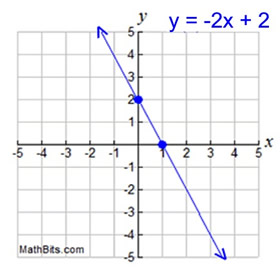
y = -2x + 2
y = -2(0) + 2; y = 2 y-intercept: (0,2)
(You can also read the y-intercept, b, from the function equation
if it is
in y = mx + b form.)
 To find the x-intercept, look where y = 0. To find the x-intercept, look where y = 0.
Remember: the x-intercept will have a y-coordinate of 0.
y = -2x + 2
0 = -2x + 2; 2x = 2; x = 1 x-intercept: (1,0)
|
|

When looking for sections of a graph that are increasing or decreasing, be sure to look at (or "read") the graph from left to right.
 Increasing: A function is increasing, if as x increases (reading from left to right), y also increases. Increasing: A function is increasing, if as x increases (reading from left to right), y also increases.
In plain English, as you look at the graph, from left to right, the graph goes up-hill. The graph has a positive slope.
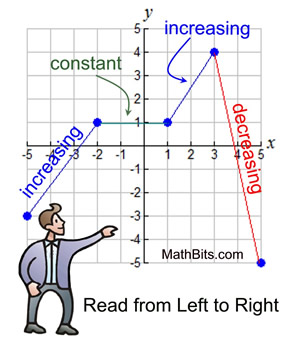
Example: The function (graph) at the right is increasing from the point (-5,-3) to the point (-2,1), which is described as increasing when -5 < x < -2 .
It also increases from the point (1,1) to the point (3,4), described as increasing when 1 < x < 3.
|
|
 Decreasing: A function is decreasing, if as x increases (reading from left to right), y decreases. Decreasing: A function is decreasing, if as x increases (reading from left to right), y decreases.
In plain English, as you look at the graph, from left to right, the graph goes down-hill. The graph has a negative slope.
Example: The graph shown above is decreasing from the point (3,4) to the point (5,-5), described as decreasing when 3 < x < 5.
 Constant: A function is constant, if as x increases (reading from left to right), y stays the same. Constant: A function is constant, if as x increases (reading from left to right), y stays the same.
In plain English, as you look at the graph, from left to right, the graph goes flat (horizontal). The graph has a slope of zero.
Example: The graph shown above is constant from the point (-2,1) to the point (1,1), described as constant when -2 < x < 1. The y-values of all points in this interval are "one".
 |
Intervals of increasing, decreasing or constant ALWAYS pertain to x-values.
Do NOT read numbers off the y-axis.
Stay on the x-axis for these intervals!
|

 |
 |
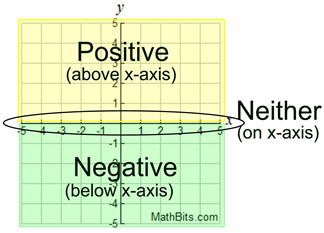
y-values positive
or
y-values negative |
 |
Secret to Finding the Intervals!
The secret to correctly stating the intervals where a function is positive or negative is to remember that the intervals ALWAYS pertain to the locations of the x-values. Think of reading the graph from left to right along the x-axis.
Do NOT read numbers off the y-axis for the intervals. Stay on the x-axis!
|

When you are working with word problems associated with functions, you may be asked to find the largest (or smallest) y-value from the graph. These values are referred to as the maximum (or minimum) values of the function.
 Linear Graphs Linear Graphs
A straight line is the easiest graph for determining the maximum and minimum values.
If a question is asking for the largest (or maximum) value obtained by the graph, it is looking for the largest y-value.
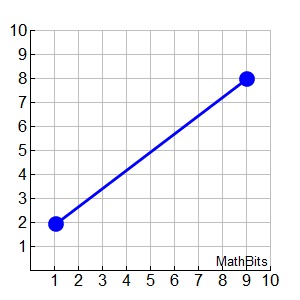
For a graph, such as the one at the right, it would be stated that what you are seeing is the entire graph. You do not have to worry that there are more points that you are not seeing.
For the line at the right, it maximum value is 8 and its minimum value is 2.
|
 |
 Non-Linear Graphs Non-Linear Graphs
For non-linear graphs, you may have to look for "turning points" in the graph.
A "turning point" on a graph is a point at which the graph changes from increasing to decreasing (it looks like a "hill"), or from decreasing to increasing (it looks like a "valley").
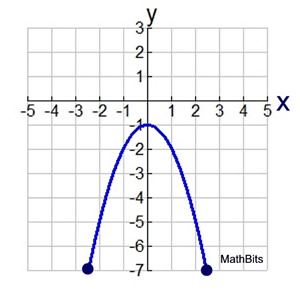
For the graph at the right (which is the entire graph), the turning point is at the top of the "hill" at the point (0,-1).
The maximum value is -1 and the minimum value is -7.
|
 |
 Split Graphs Split Graphs
Split graphs may be comprised of linear portions and non-linear portions.
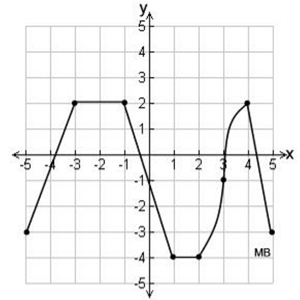
Look carefully at these graphs to see where the largest and smallest y-values fall.
For this graph (which is the entire graph), there is more than one point that represents the maximum value, all of which have a value of 2.
There is also more than one point that represents the minimum value, all of which have a value of -4.
|
 |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|