|
Directions: Read carefully.
1. |
The line through points A, B, and C is a straight line.
If m∠ABD = 124º, find the m∠CBD.
Choose:
|
|
|
2. |
Two vertical angles are expressed as
62 and 2x - 20.
Find the value of x.
Choose:
|
 |
|
3. |
∠ABD and ∠CBD are adjacent angles.
If m∠ABD = 36º and m∠ABC = 67º,
find m∠DBC.
Choose:
|
|
|
4. |
Two complementary angles are expressed as
2x + 13 and 3x - 18. Find the value of x.
Choose:
|
|
|
5. |
The ratio of m∠CBE to m∠ABD to m∠DBE is 1 : 2 : 3 as shown.
∠ABC is a straight angle.
Find m∠ABD.
Choose:
|
|
|
|
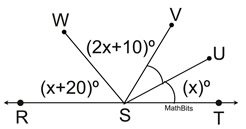
6. |
As seen in the diagram at the right:
m∠RSW = x + 20; m∠WSV = 2x + 10,
m∠UST = x; m∠VSU = m∠UST.
Find m∠WSV.
Choose:
|
straight ∠RST |
|
7. |
Diagram as shown and labeled.
a) Find x.
Choose:
b) Find m∠CMB.
Choose:
|
|
|
8. |
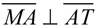 The angles are represented as shown.
The angles are represented as shown.
Find m∠HAT
Choose:
|
|
|
9. |
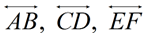
intersecting at H.
Find x and y.
Choose:
|
|
|
10. |
In the diagram at the right,
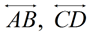
and angles are labeled.
Find m∠CEB.
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|