|
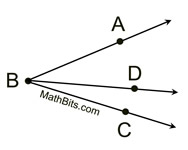
If D lies in the interior of ∠ABC, then
m∠ABD + m∠DBC = m∠ABC. |
This concept may also be referred to as
"whole quantity" or "the whole is equal to the sum of its parts." |
 |
|
An angle bisector is a ray from the vertex of the angle into the interior of the angle forming two congruent angles (angles of equal measure).
|
|
| |
|
|
Remember that the word "bisect" means to cut into two equal pieces. |
Angles Forming a Straight Line |
If the non-shared sides of two, or more, adjacent angles form a straight line, the measures of the angles add up to 180º.
|
|
| |
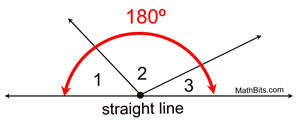
m∠1 + m∠2 + m∠3 = 180º
|
This is a "common sense" rule. A straight line is also a straight angle, which contains 180º. If these angles are adjacent (don't overlap), and their non-shared sides form a straight line, the angles comprise a straight angle which contains 180º. |
If two, or more, adjacent angles completely surround a point, the measures of the angles add up to 360º.
|
|
| |
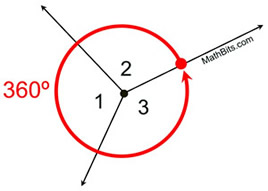
m∠1 + m∠2 + m∠3 = 360º
|
This is also a "common sense" rule. The complete revolution around a point is a circular 360º. If these angles are adjacent (don't overlap), and together they form one complete revolution, the measures of the angles will total 360º. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|