|
|
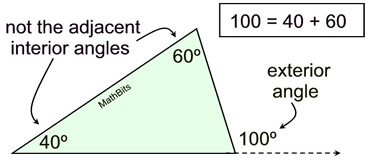
An exterior angle of a triangle is an angle formed by one side of the triangle and the extension of an adjacent side of the triangle.
|
|
|
FACTS:
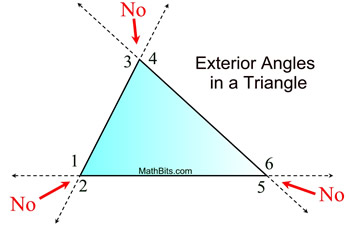
• Every triangle has 6 exterior angles, two at each vertex.
• Angles 1 through 6 are exterior angles.
• Notice that the "outside" angles that are "vertical" to the angles inside the triangle are NOT called exterior angles of a triangle.
|
|
The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles.
(Non-adjacent interior angles may also be referred to as remote interior angles.) |
|
|
FACTS:
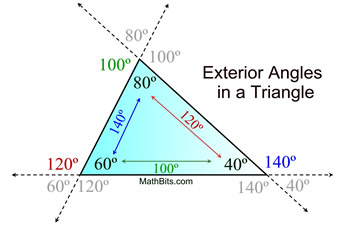
• An exterior ∠ is equal to the addition of the two
Δ angles not right next to it.
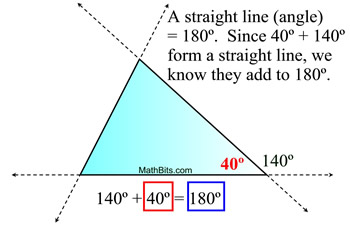
140º = 60º + 80º;
120º = 80º + 40º;
100º = 60º + 40º
• An exterior angle is supplementary to its adjacent Δ angle. 140º is supp to 40º
• The 2 exterior angles at each vertex are = in measure because they are vertical angles.
• The exterior angles (taken one at a vertex) always total 360º
|

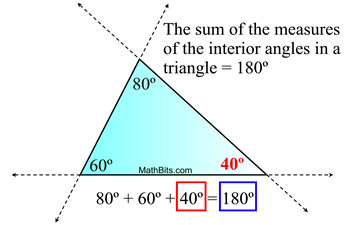
So, how do we know that this theorem is true?
This theorem is connected to the theorem that states "the sum of the measures of the angles of a triangle = 180º ", and the concept that a straight line (angle) = 180º.
Let's take a look:
If we pull the two equation statements together, we can see the connection:

The 140º can replace the 80º + 60º.
In other words, the exterior angle's measure is the same as the measures of the two non=adjacent interior angles added together.

There is a "common sense" inequality theorem about exterior angles:
|
The measure of the exterior angle of a triangle is greater than the measure of either non-adjacent interior angle. |
|
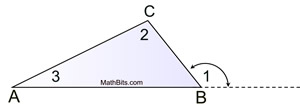
In the diagram at the right,
∠1 is an exterior angle for ΔABC.
Since, by the previous theorem, m∠1 = m∠2 + m∠3,
it is common sense that m∠1 > m∠ 2
and m∠1 > m∠3.
|
|

1. 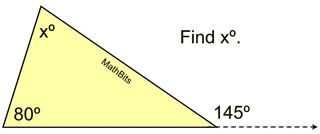 |
Solution: Using the Exterior Angle Theorem
145 = 80 + x
x = 65
Now, if you forget the Exterior Angle Theorem, you can still get the answer by noticing that a straight angle has been formed at the vertex of the 145º angle. See Example 2. |
2. 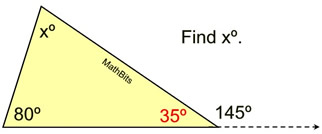 |
Solution: "I forgot the Exterior Angle Theorem."
The angle adjacent to 145º will form a straight angle along with 145º adding to 180º. That angle is 35º.
Now use rule that sum of ∠s in Δ = 180º.
35 + 80 + x = 180
115 + x = 180
x = 65 |
3. 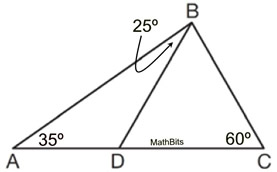 |
Find m∠DBC.
When a diagram contains more than one triangle, an exterior angle can exist as an interior angle from another triangle.
Solution:∠BDC is an exterior angle for ΔABD.
m∠BDC = 35 + 25
m∠BDC = 60º
180 = m∠DBC + 60 + 60
m∠DBC = 60º
Alternative solution using the fact that the measures of the angles in
ΔABC add to 180º.
m∠A + m∠C + m∠DBC + m∠DBA = 180º
35º + 60º + m∠DBC + 25º = 180º
120º + m∠DBC = 180º
m∠DBC = 60º
|
4. 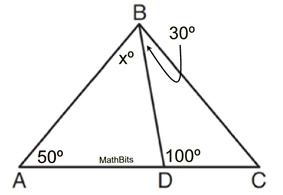 Find xº.
Use the fact that the 100º∠ can be an exterior angle for
ΔADB.
Find xº.
Use the fact that the 100º∠ can be an exterior angle for
ΔADB.
Solution:
100 = x + 50
x = 50º
Alternative solution using the fact that the measures of the angles in
ΔABC and ΔDBC each add to 180º.
Find
m∠C. 30º + 100º +
m∠C = 180.
m∠C = 50º
Now, use m∠A + m∠C + m∠DBC + m∠DBA = 180º
50º + 50º + 30º + xº = 180º
130º + x = 180º
x = 50º
Alternate solution using a linear pair: Find that m∠ADB = 80º. The use the sum of the angles ΔADB to find x.
|
5.
|
|
Solution:
1) Exterior Angle Theorem - TRUE
2) Inequality Theorem about Exterior Angles (stated above) - TRUE
3) Linear Pairs are supplementary (2 ∠s adding to 180) - TRUE
4) FALSE (it should read m∠1 > m∠C) |
| |
Given ΔABC as shown.
Which statement is NOT true?
1) m∠1 = m∠A + m∠C
2) m∠1 > m∠A
3) m∠1 + m∠ABC = 180º
4) m∠1 < m∠C |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|