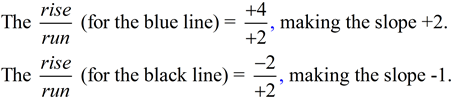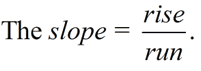|
When you start graphing lines, you can see that lines change in direction and in steepness.
As you move from left to right across the graph, ...
• direction is whether the line is going up or down as you move.
• steepness is how fast the line is going up or down. |
|
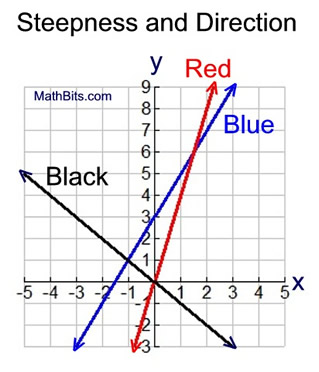
The Blue line gradually increases, goes up, as you move from left to right.
The Red line is rising more quickly than the blue line, as you move from left to right. It is "steeper" than the blue line.
The Black line appears to have a more gentle steepness, but it is going "down" (decreasing), as you move from left to right, instead of going "up" (increasing) like the other two lines.
There is a value, called the "slope" that will tell us the direction (whether the line is going up or down), and the steepness (how fast the line is going up or down).
|
| How do you determine the slope of a line? |
The direction of a line can be determined by looking at the graph of the line.
(It can also be determined by the labeling placed on directional counting when finding slope, as we will see below.)
"Direction" in relation to slope:
If the line goes up (increases) as you go from left to right, the slope will be positive.
If the lines goes down (decreases) as you go from left to right, the slope will be negative.
|
To find the steepness of a line, we are going to compare the line's increase in horizontal distance on the graph between points, with its increase in vertical distance between those same points. To do this we are going to draw some right triangles that will connect points along the line.
Linear equation: y = 3x
Prepare a table of values to get ordered pairs for plotting the line.
x- value |
y-value |
ordered pair
(x, y) |
-2 |
-6 |
(-2, -6) |
-1 |
-3 |
(-1, -3) |
0 |
0 |
(0, 0) |
1 |
3 |
(1, 3) |
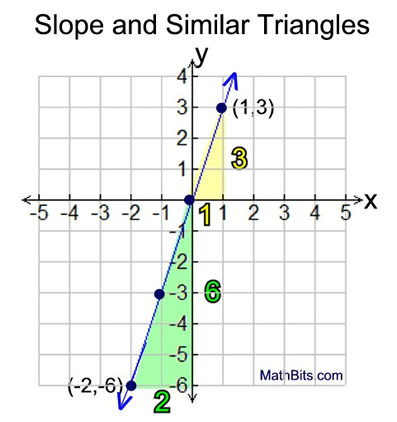
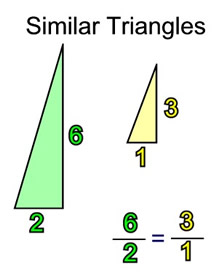
In the yellow triangle on the graph, to get from point (0,0) to point (1,3), we moved 1 horizontal grid unit to the right, and 3 vertical grid units up. |
|
Yellow Triangle(between (0,0) and (1,3):
Vertical increase (rise) of 3 grid units.
Horizontal increase (run) of 1 grid unit.
Green Triangle (between (-2,-6) and (0,0):
Vertical increase (rise) of 6 grid units. Horizontal increase (run) of 2 grid units.
|
The vertical change is called the "rise"
The horizontal change is called the "run".
|
 Straight lines that pass through the origin, such as the graph above,
show a proportional relationship. The slope of such a line can be referred to as
the constant of proportionality (the unit rate).
Graph pattern:
When x increase 1 unit, y increases 3.
When x increases 2 units, y increases 6.
When x increases 3 units, y increases 9.
When x increases by a units,
y increases by 3a units.
The ratio of the increase across a line is always the same. In this case, the ratio is 3 to 1.
|
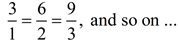
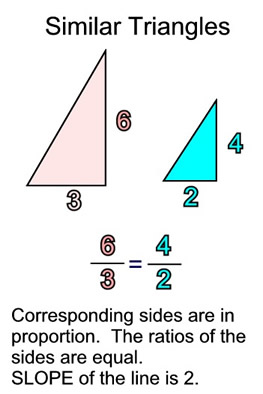
It does not matter how big or small the triangles are that connect points on a straight line. ALL of the triangles drawn on the same line will be similar triangles and the ratios of their sides will be equal.
There is a graph pattern of movement along a straight line. In the example above, if you increase one x-unit to the right, the y-unit increase 3 units up. This pattern is "the y-unit increase up will always be three times the x-unit increase to the right."
In these triangles, the ratio of this vertical increase (rise) to the horizontal increase (run) will always be the same, or 3 to 1, making the slope = 3.
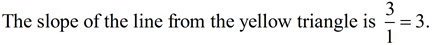
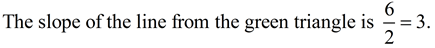
(Note: The slope of the line is positive because the line in increasing
as you move from left to right.)
|
"Steepness" in relation to slope:
The steeper the line is when moving from left to right, the larger the value of its slope.
(The word "value" in this context, refers to the "absolute value" of the slope,
not taking into account its positive or negative direction.) |
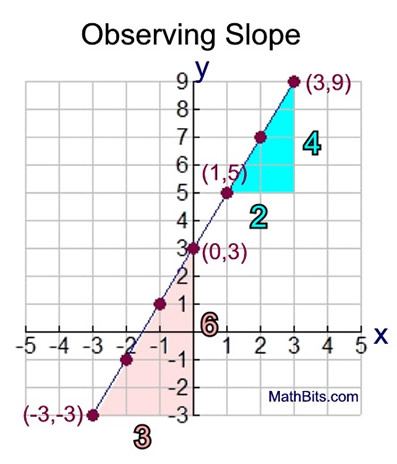
Let's that a look at a line that does not go through the origin.
(The process will be the same. Just be more careful on the counting.)
Linear equation: y = 2x + 3
Prepare a table of values to get ordered pairs for plotting the line.
x- value |
y-value |
ordered pair
(x, y) |
-3 |
-3 |
(-3, -3) |
-2 |
-1 |
(-2, -1) |
-1 |
1 |
(-1, 1) |
0 |
3 |
(0, 3) |
1 |
5 |
(1, 5) |
2 |
7 |
(2, 7) |
3 |
9 |
(3, 9) |
In the red triangle, to get from point (-3,-3) to point (0,3), we move 3 horizontal grid units to the right, and 6 vertical grid units up. A rise of 6 and a run of 3. |
|
Blue Triangle (between (1,5) and (3,9):
Vertical increase (rise) of 4 grid units.
Horizontal increase (run) of 2 grid units.
Slope of the line from blue triangle 4/2 = 2.
Red Triangle (between (-3,-3) and (0,3):
Vertical increase (rise) of 6 grid units.
Horizontal increase (run) of 3 grid units.
Slope of the line from the red triangle 6/3 = 2.
|
|
| Various ways to count vertical/horizontal distances: |
We know that distance is a "positive" concept. The measurement of "-24 inches" does not make any sense. But ... when working with slope, we can label the "direction" of our vertical and horizontal measurements when we are counting on the graph.
Remember: To measure the slope from a triangle, you start at one point on the line and walk along the horizontal and vertical sides of the triangle in a continuous pattern until you reach the other point.
 |
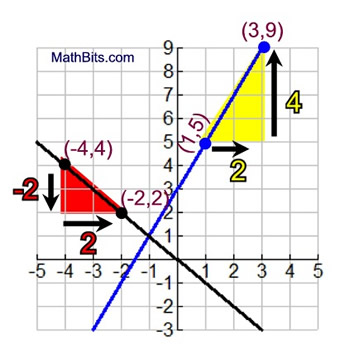In the yellow triangle on the blue line, the example shows walking from (1,5) to the right, then walking up to (3,9).
| Distances measured by counting to the "right" or "up" can be labeled as positive values. |
In the red triangle on the black line, the example shows walking from (-4,4) down, then walking to the right to (-2,2).
| Distances measured by counting "down"
or to the "left" can be labeled as negative values. |
|
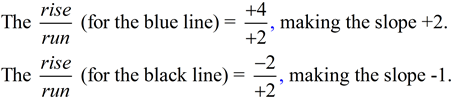
Note: Distances can be counted starting at either (triangle) vertex point on the line. Just remember to continue your journey along the outside of the triangle until you arrive at the other vertex point on the line. See the options below.
Starting at point (1,5):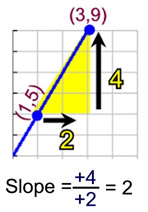
Moving to the "right" and "up" are positive movements.
Rise = 4 and run = 2.
|
Starting at point (3,9):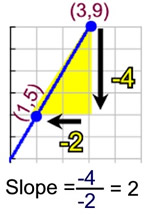
Moving "down" and to the "left" are negative movements
Remember a negative divided by a negative is positive.
Rise = -4 and run = -2.
|
Starting at point (-4,4):
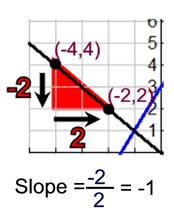Moving "down" is negative movement, and moving "right" is positive movement.
Rise = -2 and run = 2.
|
Starting at point (-2,2):
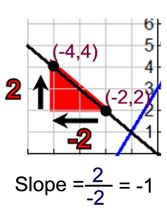Moving "left" is negative movement, and moving "up" is positive movement.
Rise = 2 and run = -2.
|
Either method of walking (and counting) along the sides of the triangle yields the same results.
The slope of the blue line is 2. |
The starting point makes no difference.
The result will be the same either way.
The slope of the black line is -1. |
Did you notice that the final slope answer is not labeled in any type of units?
There is no labeling such as inches, feet, centimeters, pounds, etc. for slope.
(You may see labeling in application problems in keeping with the text of the problem.)
| In Summary:
The slope of a line tells us the direction of the line (increasing across the graph, or decreasing), as well as the steepness of the line. Steepness can also be referred to as incline, pitch, or grade (gradient). In the next lesson, the slope will be referred to as the "rate of change".
"SLOPE" is an extremely important concept in mathematics.
It will follow you throughout your future studies, and is a worthy topic to be remembered. |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
