Lines of the form y = mx pass through the origin.
 Slope is traditionally designated by the letter "m"
Slope is traditionally designated by the letter "m".
We know that the ratio of vertical increase to horizontal increase creates the slope of the line.
We also know that this ratio is constant (does not change) along the line.
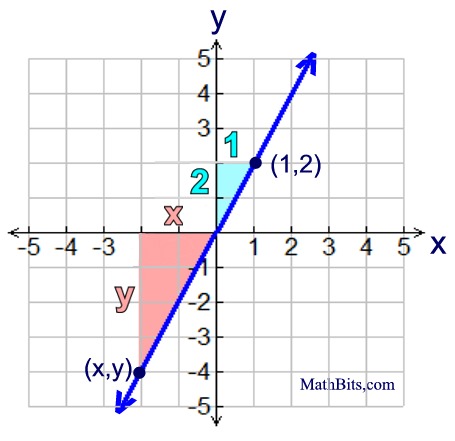 We have now shown that y = 2x is the equation of
this line with a slope of 2 and passing through (0,0). We have now shown that y = 2x is the equation of
this line with a slope of 2 and passing through (0,0). |
Given: slope of line = 2
Starting at the origin (0,0), we can draw a blue triangle with a rise of 2 and a run of 1 to illustrate this slope.
ALL triangles drawn on this line will now have a ratio of 2 to 1 for vertical increase to horizontal increase.
Let's draw a new triangle and label it's horizontal increase as x and its vertical increase as y.
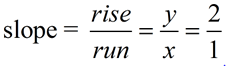
(multiply both sides by x)
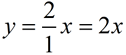
|

Now that we have the idea as to how we can establish the equation of a line by examining its slope, let's try to establish a more general formula. Remember that slope will be designated by m.
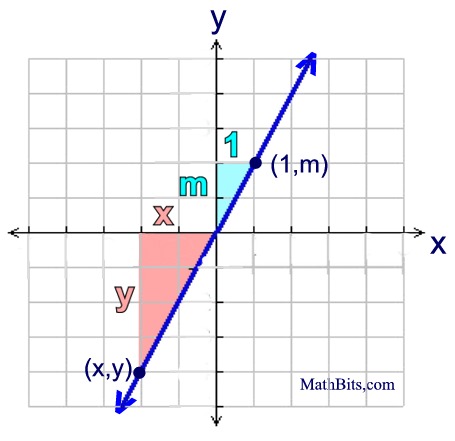 We have now shown that y = mx is the equation of
this line with a slope of m and passing through (0,0). We have now shown that y = mx is the equation of
this line with a slope of m and passing through (0,0). |
Given: slope of line = m
We are examining the same process again, only this time we are calling the slope "m" rather than assigning it a specific value.
Since the two triangles are similar we can set the ratios of their corresponding sides equal (forming a proportion).
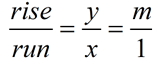
(multiply both sides by x)
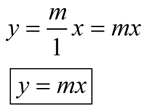
|

Lines of the form y = mx + b do no pass through the origin, unless b = 0.
 Slope is designated by the letter "m" and "b" represents the y-intercept.
Slope is designated by the letter "m" and "b" represents the y-intercept.
This approach will be similar to what we saw in the y = mx derivation.
Look carefully, as the work on the graph is a bit more complicated in this y = mx + b derivation.
|
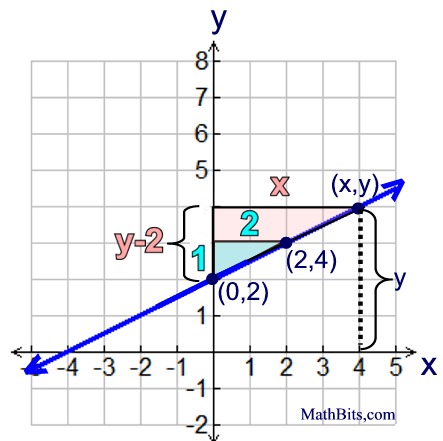
Given: slope of line = 1/2
We will be starting at the point (0,2) where the line crosses the y-axis for both of our triangles. This point is called the y-intercept, and is traditionally labeled as (0,b).
We can draw a blue triangle with a rise of 1 and a run of 2 to illustrate the given slope.
 We can NOT label the left side of the red triangle as simply y, because y represents the distance from the x-axis up to the top of the red right triangle. We can NOT label the left side of the red triangle as simply y, because y represents the distance from the x-axis up to the top of the red right triangle.
The left side of the red triangle is actually y - 2.
|
Set up the ratios
to form the proportion.
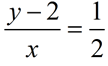
|
|
(Multiply both sides by x.
Then add 2 to both sides.)
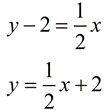
|
CONCLUSION: We have now shown that y = ½ x + 2 is the equation of
this line
with a slope of 2 and passing through (0,2).
|

Now for the more general form.
Remember that the slope will be designated by m, and the y-intercept by b.
|
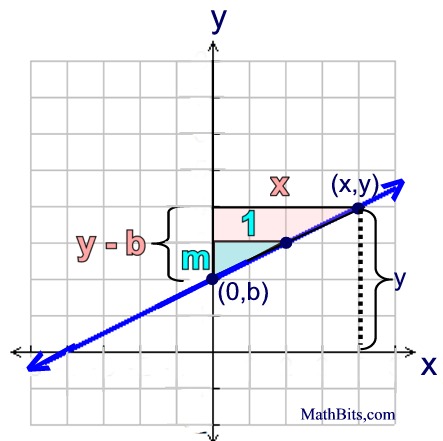
Given: slope of line = m
We will be starting at the point (0,b) where the line crosses the y-axis for both of our triangles. This point is called the y-intercept, and is traditionally labeled as (0,b).
We can draw a blue triangle with a rise of m and a run of 1 to illustrate the given slope of m.
 We can NOT label the left side of the red triangle as simply y, because y represents the distance from the x-axis up to the top of the red right triangle. We can NOT label the left side of the red triangle as simply y, because y represents the distance from the x-axis up to the top of the red right triangle.
The left side of the red triangle is actually y - b.
|
Set up the ratios
to form the proportion.
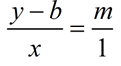
|
|
(Multiply both sides by x.
Then add b to both sides.)
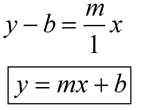 |
CONCLUSION: We have now shown that y = mx + b is the equation of
this line
with a slope of m and passing through (0,b).
|
 The formula y = mx + b is an important formula.
You will need this formula for future studies in mathematics. |


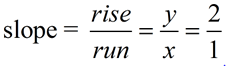
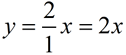

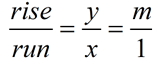
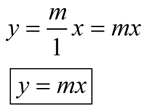
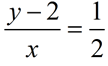
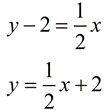
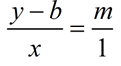
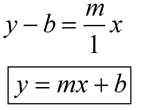
 The formula
The formula