A linear equation is an equation whose solutions form a straight line on the coordinate plane.
(Linear = Line) |
Linear equation: y = 2x + 3
Solutions as seen in a table:
These x and y values make the equation true.
x- value |
y-value |
ordered pair
(x, y)
|
-3 |
-3 |
(-3, -3) |
-2 |
-1 |
(-2, -1) |
-1 |
1 |
(-1, 1) |
0 |
3 |
(0, 3) |
1 |
5 |
(1, 5) |
2 |
7 |
(2, 7) |
3 |
9 |
(3, 9) |
|
When the ordered pairs are plotted
on a graph (the coordinate plane), a straight line will be formed.
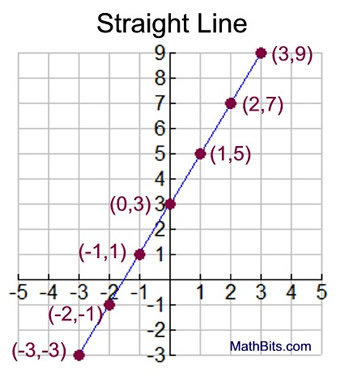
Any point on this line is a solution
to the equation y = 2 x + 3. |
We can see from the example above, that our linear equation can be viewed three ways:
as an equation, as a list of ordered pairs in a table, and as a graph.

Let's look at an application problem.
Mr. Carpenter is driving his car down a highway at a constant speed of 65 mph.
The equation to determine the distance he has traveled is d = 65t
where d = distance traveled in miles
and t = the time traveled in hours. |
 |
The Table of Ordered Pairs:
t - value
(hours)
|
d-value
(miles)
|
ordered pair
(t, d) |
0 |
0 |
(0,0) |
1 |
65 |
(1,65) |
2 |
130 |
(2,130) |
3 |
195 |
(3,195) |
4 |
260 |
(4, 260) |
8 |
520 |
(8, 520) |
10 |
650 |
(10, 650) |
|
The Graph of Distance Traveled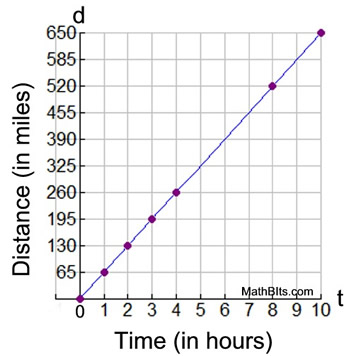
|
• The graph for this problem only shows the first quadrant, where the values of time and distance are positive. In real world problems, time and distance are positive quantities.
• Any ordered pair on the graphed line will be a solution to the equation d = 65t.
• Note that the scale on the t-axis is one unit and the scale on the d-axis is 65 units.
• Note that for every hour traveled, the distance traveled increases by 65 miles.
• Since the distance traveled is dependent upon the amount of time Mr. Carpenter drives, d is the dependent variable in this problem and t is the independent variable.



