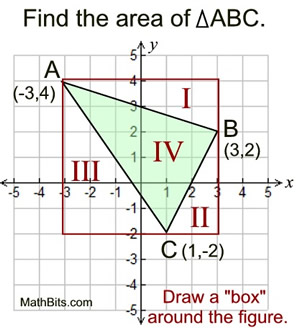
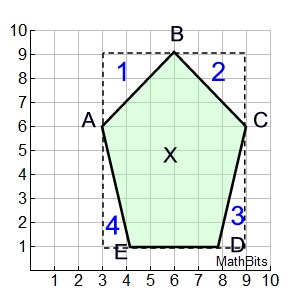
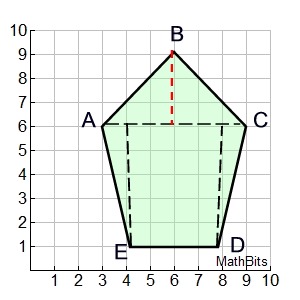
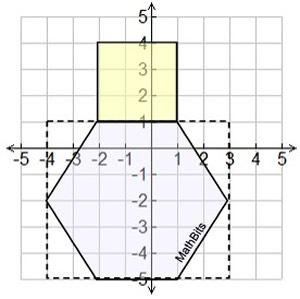
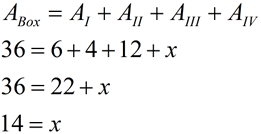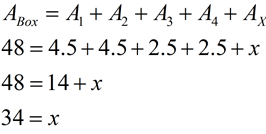logo


Composing Polygons to find Area



Composing (or composition) is the process of putting together two or more shapes to form a new shape. Drawing a composite figure can be helpful when determining the area of a polygon.

This section will be "composing" polygons into rectangles as a strategy for finding the area of the polygon. We have already used this concept when we created a "box" around a figure graphed in the coordinate plane, so we could easily find its area.
Note: the "refresher" example below reflects our previous work with composing.

Refresher:
box2

• The smallest "box" possible was drawn to enclose the polygon (ΔABC) and create a drawing with 3 right triangles "attached" to the triangle. The "box" must follow the grids of the graph paper.

• Each section of the box was numbered with a Roman numeral (axes are ignored when numbering).

• "The whole is equal to the sum of its parts." The area of each of the parts of the "box" added together equals the area of the "box".
boxarea2
The answer is 14 square units.
When the "box" is drawn around the triangle, shapes whose areas can be found by simply counting are created. The "box's" area can be found by counting, and the areas of right triangles I, II, and III can all be found by counting. Our task was simplified by using this "box" method.

 

ex1 Find the area of pentagon ABCDE.

Solution: You can tell by looking, that this pentagon is not a "regular" pentagon. But, that is not a problem as the "box" method works for all forms of polygons.
• Draw the box.
• The outer triangles have been numbered with integers this time, and ABCDE will be called X.
greenpentans
The answer is 34 square units.
greenpentgrid

dividerdash


This particular problem lends itself to also being easily solved by "decomposing",
so let's take a look at that solution also.
ex2 Find the area of this pentagon by decomposing it into recognizable shapes.


Solution: The pentagon can be divided into ΔABC and trapezoid ACDE. The trapezoid can then be broken down further into two triangles and a rectangle.
• The area of ΔABC = ½(6)(3) = 9 sq. units.
• The area of the rectangular part of the trapezoid = 4 x 5 = 20 sq. units.
• Each of the small Δs in the trapezoid has an area of ½(1)(5) =2.5 sq. units.
The total area is
9 + 20 + 2(2.5) = 34 square units.
(Same result as was seen in Example 1.)


greenoentde

dividerdash
ex3 Find the area of this composite figure made up of an irregular hexagon and a square.


Solution: Finding the area of the square is easy.
• Area of square = 3 x 3 = 9 sq. units
Finding the area of the hexagon is a bit more tricky. Let's compose further and form a rectangle around the outside of the hexagon.
• The 4 right triangles surrounding the hexagon are all of the same area: ½(3)(2) = 3 sq. units each.
• The area of the rectangle we drew is 6 x 7 = 42.
• Subtract the area of the four right triangle from the area of the rectangle to get the area of the hexagon. 42 - 4(3) = 42 - 12 = 30 sq. units.
• The area of the hexagon plus the area of the square = 30 + 9 = 39 sq. units.
hexsquaregrid


divider


NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".