|
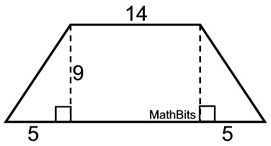
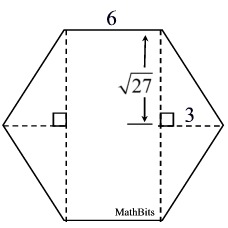
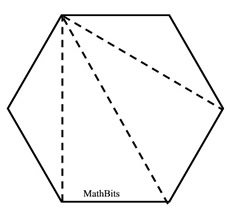
Find the area of this regular hexagon which has been decomposed. Round answer to nearest tenth of a sq. unit. |
Solution:
A regular hexagon has 6 sides of equal length.
The hexagon has been divided into 4 small right triangles and one rectangle.
• The area of the 4 right triangles is ½(5.196)(3)=7.794 sq. units for each triangle
• The area of the rectangle is 2(5.196)(6)=62.352 sq. units.
Total area = 4(7.794) + 62.352 = 93.528 = 93.5 sq.units
|
|
|
 |
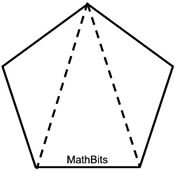
Find the sum of the measures of the interior angles of a pentagon. |
Solution: The same strategy that was used with the quadrilateral in the refresher above, will be used here.
A pentagon has 5 sides. Draw as many diagonals as possible from the same vertex, to decompose the pentagon into three triangles.
A pentagon is now composed of three triangles, each having the sum of their angles = 180º.
The sum of the interior angles of a pentagon will be 3 x 180 = 540º.
|
|
|
 |
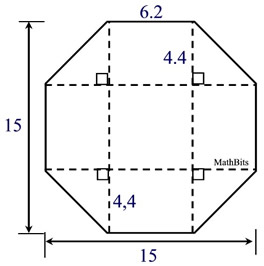
Find the area of this regular octagon which has been decomposed. |
Solution: The regular octagon (with all 8 sides of = length) is divided into 5 rectangles and 4 triangles.
• Each of the small Δs has an area of ½(4.4)(4.4) = 9.68
sq. units each.
• The square in the center is 6.2 x 6.2 with an area of 38.44 sq. units.
• The 4 remaining rectangles are 4.4 x 6.2 with an area of 27.28 sq. units each.
The total area is
4(9.68) + 38.44 + 4(27.28) = 186.28 square units.
|
 Lengths have been given to nearest tenth.
Lengths have been given to nearest tenth. |
|
 |
Find the number of degrees in each interior angle of a regular hexagon. |
Solution: In Example 2, we saw how to decompose the pentagon into triangles by drawing diagonals from one vertex. Using this same strategy in a 6-sided hexagon, produces 4 triangles. 4 x 180 = 720º.
The sum of the measures of the angles in a hexagon is 720º.
Because this is a "regular" hexagon, we know that all of its angles are of the same measure.
If we divide 720 by 6, we find that each interior angle has a measure of 120º.
|
|
|
 |
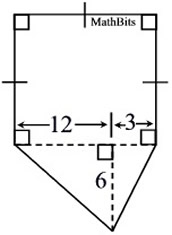
Find the area of this irregular pentagon which has been decomposed. |
Solution: This irregular pentagon has been decomposed into a square and a triangle. While not ALL of its sides are the same length, the hash marks tell us that 3 of them are the same length.
• The area of the square is 15 x 15 = 225 sq. units.
• The are of the triangle is ½(6)(15) = 45 sq. units.
The total area = 225 + 45 = 270 sq. units. |
|