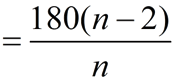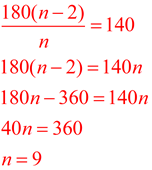|
The interior angles of a polygon are the angles at each vertex on the inside of the polygon.
Some interior angles are well known and/or easy to find.
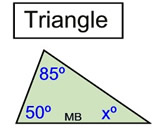We have proven that the sum of the measures of the interior angles of a triangle is 180º.
We can easily find that xº = 45º. |
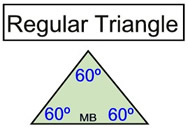A regular triangle is an equilateral triangle with all sides and angles of equal measure. We only need to divide 180 by 3 to find the size of each angle. |
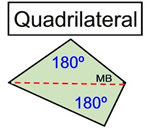When dealing with 4-sided polygons, a diagonal divides the figure into two triangles showing that the sum of the interior angles must be 2•(180) = 360º. |
The strategy shown above in the quadrilateral, of dividing the figure into triangles, will be used to investigate the interior angles of polygons with more than four sides.
This strategy may be referred to as "decomposing", "partitioning", or "dissecting".
If we use diagonals to partition a polygon into a series of triangles (as was done with the quadrilateral),
we can calculate the sum of the interior angles of larger-sided polygons.
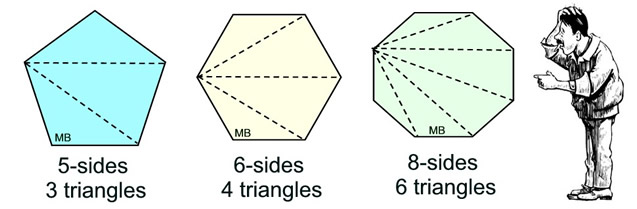
How many triangles, formed using diagonals, make up the polygon?
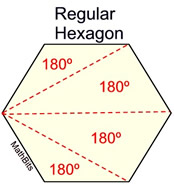
In a regular hexagon, four triangles can be created using diagonals of the hexagon from a common vertex. Since the interior angles of each triangle totals 180º, the hexagon's interior angles will total 4•(180º), or 720º.
|
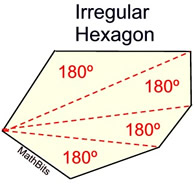
This same approach can be taken in an irregular hexagon. The diagonals form four triangles whose interior angles total 180º, giving the hexagon's interior angles a total of 4•(180º), or 720º.
|
Notice that the sum of the interior angles is the same
for both the regular and the irregular hexagons.
Also notice that we formed 4 triangles in the hexagon (with 6 sides).
Yes! There is a pattern!
The number of triangles from 1 vertex will be
2 less than the number of sides, n, of the polygon, or n - 2 triangles.
This pattern leads to a formula!
The sum of the interior angles is 180º • (the number of triangles formed)
or 180•(n - 2).
|
The pattern developed in the example above, is consistent (true) for ALL polygons
(both regular and irregular polygons)
.
Sum of Interior Angles
of any Polygon |
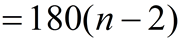(where n = number of sides) |
|
Special CASE: If you know that the polygon is a regular polygon,
you can find each interior angle by dividing by the number of sides.
(Remember that the interior angles of a regular polygon are equal in measure.)
Each Interior Angle
of a Regular Polygon |
|
|
 |
You can NOT use this formula to find each angle in an irregular polygon. Since each angle of an irregular polygon may be of different size, there is no formula for finding individual angle measures. |
|
When working with angle formulas for polygons, be sure to read carefully to determine what you are being asked to find.
Look for "hint" words such as sum, interior, each, degrees and sides. |
|
Finding SUM and EACH interior angles, with and without formulas:
 |
Find the number of degrees in the sum of the interior angles of a decagon. |
| |
So, we can draw 8 triangles in a 10-sided decagon, each with 180º for a total of 1440º.
OR, we can use the formula, where n = 10:
180(n - 2) = 180(10 - 2) = 180(8) = 1440º.
|
 |
How many sides does a polygon have if the sum of the interior angles is 1080º? |
| |
First, let's figure this out by thinking about the number of triangles you would need to get a total of 1080º for the sum of all the angles.
1080º divided by 180º = 6 (meaning 6 triangles).
If the figure divides into 6 triangles, it must have 8 sides.
OR, we can use the formula and algebra to get this answer:
Set the formula equal to 1080 and solve for n.
180(n - 2) = 1080
180n - 360 = 1080
180n = 1440
n = 8
(if n, the answer, is not a positive integer, you will know you did something wrong. A polygon cannot have a "portion" of a side.)
|
 |
Find the number of degrees in each interior angle of a regular pentagon. |
| |
A pentagon will decompose into 3 triangles, for a total of 3•180 = 540º for all 5 angles. Since each angle is the same size in a "regular" pentagon, each angle must be 540 / 5 = 108º.
OR, use the formula and some substitution to get the answer:
This is a regular pentagon and n = 5:
|
 |
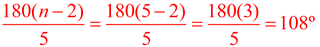
Each interior angle of a regular polygon measures 140º. Find the number of sides of the polygon. |
| |
This is a tough one! We can try "guess and check" based upon what we have seen so far for regular polygons:
• 10 sides: has total interior angles = 1440º with 144º per angle
• 8 sides: has a total interior angles = 1080º with 135º per angle
The polygon we want must be between these two. Let's try 9 sides.
Nine sides means 7 internal triangles = 1260º with 140º per angle.
YEA!! 9 sides is the answer.
OR, use the formula with some algebra:
Set the formula equal to 140 and solve for n. This solution requires use of algebraic skills.
|
|
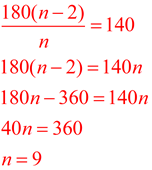
| The exterior angle of a triangle is formed by one side of the triangle and the extension of an adjacent side of the triangle. We will now extend this concept to polygons. |
 |
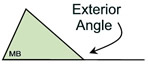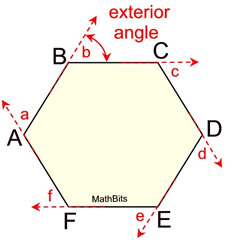
The exterior angle of a polygon is an angle that forms a linear pair
with one of the interior angles of the polygon. In the same manner as an exterior angle of a triangle, the exterior angle of a polygon is formed by any side of the polygon and the extension of its adjacent side.
The exterior angle of a polygon is formed by any side of the polygon and the extension of its adjacent side. Exterior angles and adjacent interior angles are supplementary because they form a linear pair (a straight line angle totaling 180º). If the polygon is regular, all of its exterior angles will be the same measure (because all of its interior angles are the same measure).
|
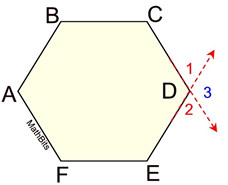
There are actually two congruent exterior angles at each vertex, but only ONE will be considered for our work. Shown below, ∠1 and ∠2 are exterior angles and are also congruent vertical angles. Note that ∠3 is NOT an exterior angle, but it is congruent to interior ∠CDE as they are vertical angles.
|
If you add ALL exterior angles (ONE at a vertex), you will get a sum of 360º.
The sum of the exterior angles of ALL polygons is a constant 360º.
We will investigate exterior angles more in future courses.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
