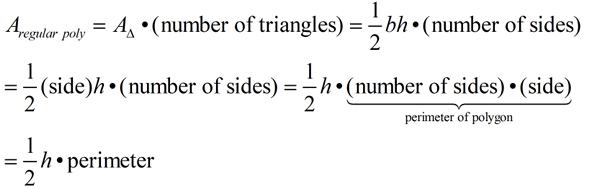|
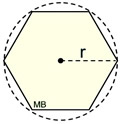
Remember that "regular" polygons have all sides congruent (equal) and all angles congruent. Regular polygons have a center and a radius. This center and radius are also the center and radius of a circle circumscribed about the outside of the polygon. Thus the term "radius". |
|
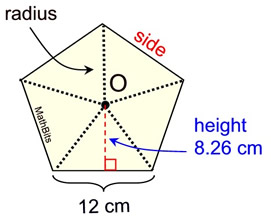
| EXAMPLE: Find the area of a regular pentagon given that each side has a length of 12 cm. and the height from the center to a side is 8.26 cm. |
|
Remember: In a regular polygon, radii drawn from the center, O, to each vertex form triangles of equal size and shape (congruent). If the height of one of these triangles is 8.26 cm., then the height of all of the triangles is 8.26 cm.
To find the area of this regular pentagon, find the area of ONE of the triangles and multiply times 5.
AΔ = ½bh = ½(12)(8.26) = 40.56 sq. cm.
For all 5 triangles: 40.56 • 5 = 247.8 sq. cm.
Area of the pentagon: 247.8 sq. cm. |
Remember, this strategy of finding the area using the triangles drawn from the center,
only works in regular polygons.
Using this strategy of partitioning (decomposing),
the areas of these regular polygons can be found
by adding together the areas of all of the congruent triangles
formed by the radii drawn to each vertex.
Since the side of the polygon is a side of the triangle,
we know that ...
the number of such triangles = the number of sides of the polygon.
We can even make a "formula" out of this knowledge:
|
 |
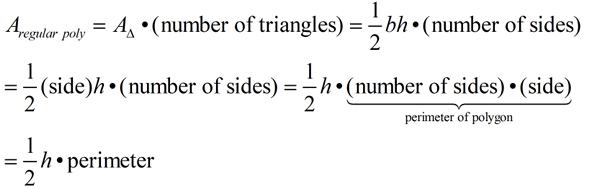
So, we know that the area of any regular polygon is
½ • (height of the triangle from the center) • (perimeter of the polygon).

FYI: As you move on in your study of Geometry, you will discover that the "height of the triangle from the center of a regular polygon" is called the " apothem" of the polygon. The formula for the area of a regular polygon can be written as A = ½a p, where a is the apothem and p is the perimeter.
 |

What about the area of irregular polygons?
|
While the method shown above for finding the area of a regular polygon works nicely, that method cannot be used on irregular polygons. Another method of finding the area using a set of coordinate axes will actually work for BOTH regular and irregular polygons. It's our old friend, the "box" method at work again. |
|
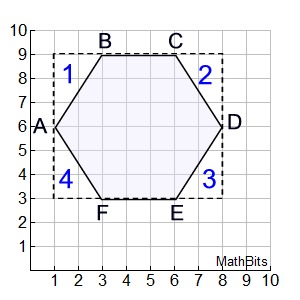
Given irregular hexagon ABCDEF with A(1,6), B(3,9),
C(6,9),
D(8,6), E( 6,3), and F(3,3).
Find the number of square units in the area of ABCDEF.
Solution: The "box method" will work nicely.
ABox = AΔ1 + AΔ2 + AΔ3 + AΔ4 + Apoly
42 = 3 + 3 + 3 + 3 + Apoly
Apoly= 30 square units
|
|
The "box method" will work with both regular and irregular polygons assuming sufficient information is given.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|