Note: Actual dimensions used on this page may be rounded to the nearest tenth of a unit.
|
Surface area is the total area that the surface of a three-dimensional object occupies, in square units. |
|
Remember: Surface area is labeled in "
square units".
Remember: "Regular" means a polygon has all of its sides of equal measure,
and all of its angles of equal measure.

This lesson will be investigating the surface area of objects
composed of polygons beyond triangles and quadrilaterals.

 Right Regular Pentagonal Prism |
|
 Use of the net is optional unless otherwise stated.
Use of the net is optional unless otherwise stated.
1. Find the surface area
of this right regular pentagonal prism.
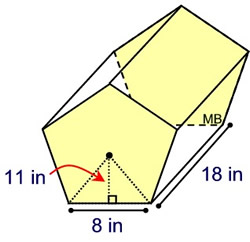
What we know about this solid:
1. There are 7 faces.
2. There are 2 congruent regular pentagons (bases) with side lengths of 8 in.
3. There are 5 rectangular lateral faces with a height length of 18 inches.
4. The height of the triangle drawn from the center (the apothem) of the pentagon is 11 in. |
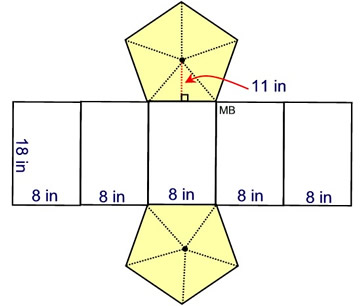
Using the net:
• Area of triangles in base of regular pentagon:
A = 5•
(½ bh)
=
5•
(½(8)(11)) = 220 (2 of these)
• Area of 5 congruent rectangles:
A = 5(8)(18) = 5•144 = 720
Surface Area = 220 + 220 + 720 = 1160 sq. in.
|
The work that was done in the example above can be combined to reveal
a "formula" for the surface area of a right regular pentagonal prism.
|
The height of the triangle drawn from the center of the pentagon
(on the base)
is called the apothem of the pentagon, and is referred to by the letter "a".
Surface area of right regular pentagonal prism:
Area of the two bases: 2 • (½ b • a)
Area of the 5 rectangles: 5 • b • h.
Formula: a • b + 5 • b • h |

 Right Regular Octagonal Prism |

2. Find the surface area
of this
right
regular octagonal prism.
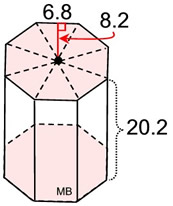
What we know about this solid:
1. There are 10 faces.
2. There are 2 congruent regular hexagons (as bases) with side lengths of 6.8 units.
3. There are 8 congruent rectangular lateral faces with height of 20.2 units.
4. Apothem of the octagon is 8.2 units. |
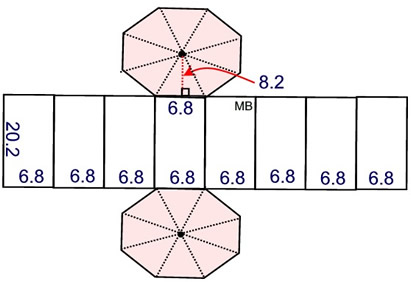
Using the net:
• Area of triangles in base of regular octagon:
A = 8•
(½ bh)
=
8•
(½)(6.8)(8.2) = 223.04 (2 of these)
• Area of 8 congruent rectangles:
A = 8(6.8)(20.2) = 1098.88
Surface Area:
2(223.04) + 1098.88 = 1544.96 sq. units
|

 Right Irregular Pentagonal Prism |
|

3. Find the surface area
of this
right
irregular pentagonal prism.
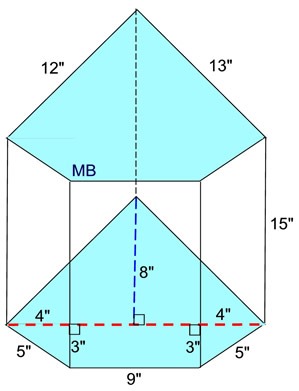
What we know about this solid:
The bases are a composite of an isosceles trapezoid and a triangle.
1. There are 7 faces.
2. There are 2 congruent bases.
3. There are 5 rectangular lateral faces of varying sizes.
4. Height of trapezoid (part of base) is 3 units.
5. Height of the prism is 15 units.
|
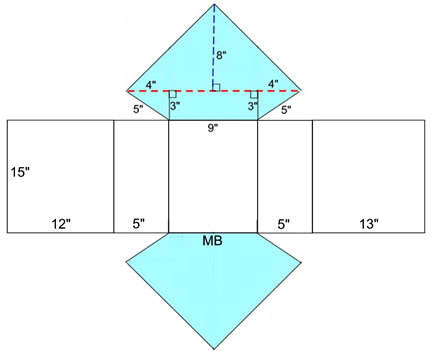
Using the net:
• Area of trapezoid part of base:
(decompose) A = 6 + 27 + 6 = 39 sq.in.
(formula) A =
½ h (b1 + b2) = ½ 3 (9 + 17) = 39 sq.in.
• Area of triangle part of base:
A = ½ (17)(8) = 68 sq.in.
Total surface area of base: 39 + 68 = 107 sq. in.
(2 of these)
• Area of 5 rectangles: (starting from net left)
A1 = (15)(12) = 180 A2 = (15)(5) = 75
A3 = (15)(9) = 135
A4 = (15)(5) = 75
A5 = (15)(13) = 195 TOTAL: 660
Surface Area: 107 + 107 + 660 = 874 sq. in.
|

In the first two examples, we used triangles drawn from the center of the regular polygons to find the apothem of the polygon and the area of the triangle. This strategy allowed us to find the area of the bases of the solids.
This method WILL NOT WORK with irregular polygons. Irregular polygons do not have a "center" that is equidistant from the polygon's sides (an apothem). They do have a "center of balance", but this location is not equidistant from the sides.
To find the area of the base in an irregular polygon, we need to hope that we can
decompose the shape into recognizable figures whose areas can be determined.

 Right Regular Hexagonal Pyramid |
|
4. Find the surface area
of this
right regular hexagonal pyramid.
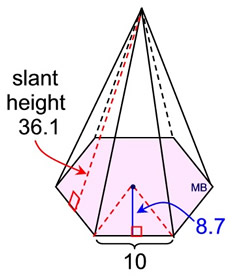
What we know about this solid:
1. There are 7 faces.
2. The regular hexagon base has side lengths of 10.
3. There are 6 congruent lateral face isosceles triangles each with a slant height of 36.1.
4. The apothem of the hexagon is 8.7.
|
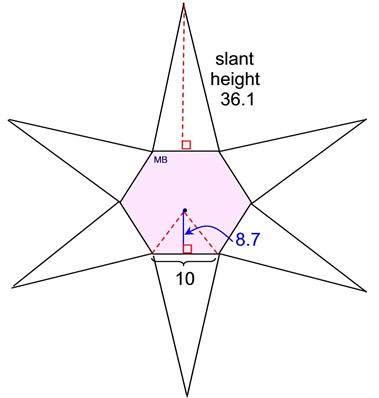
Using the net:
• Area of base regular hexagon:
ABase = 6(½(10)(8.7)) = 261
• Area of 6 congruent lateral triangles:
Alateral Δs = 6(½(10)(36.1)) = 1083
Surface area = 261 + 1083 = 1344 square units |

 Right Irregular Pentagonal Pyramid |
|
|
5. Find the surface area
of this
right trapezoidal pyramid.
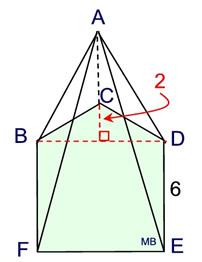
What we know about this solid:
1. The base is a composite of a square (BDEF) and a isosceles triangle ΔBCD.
2. Triangle ΔBCD has side lengths of 3.6, 3.6 and 6.
3. There are 6 faces.
4. There are 5 triangular lateral faces of varying slant heights.
5. Height of ΔBCD is 3.
6. Height of the pyramid is 10.
Note: Actual dimensions have been rounded to nearest tenth.
|
Below is information on the slant heights of the lateral faces.
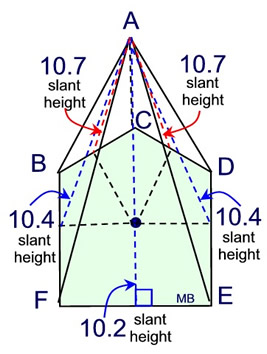
 Since the irregular pentagon base is not "regular", the slant heights in this pyramid be of varying lengths. Since the irregular pentagon base is not "regular", the slant heights in this pyramid be of varying lengths.
• Find the area of the composite base:
Area of square =36, and area of triangle
=½ (6)(2)=6, for a total area of 42 sq. units.
• Area of 5 lateral triangles:
A1 = ½(6)(10.2) = 30.6
A2 = ½(6)(10.4) = 31.2
A3 = ½(3.6)(10.7) = 19.26
A4 = ½(3.6)(10.7) = 19.26
A5 = ½(6)(10.4) = 31.2
Surface Area = 42 + 30.6 + 31.2 + 19.26 + 19.26 + 31.2 = 173.52 square units
|