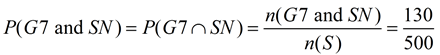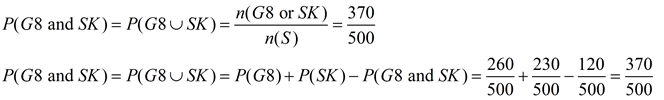We worked in the Statistics section with two-way frequency tables.
Let's take a look at how two way frequency tables are associated with probability.
Two Way Frequency Table
Students |
snowboarding |
skateboarding |
Total |
Grade 7 |
130 |
110 |
240 |
Grade 8 |
140 |
120 |
260 |
Total |
270 |
230 |
500 |
|
Let's apply our probability "vocabulary" to the table. There are four possible "events" occurring:
| G7 = Grade7 |
G8 = Grade 8 |
SN =
snowboarding |
SK =
skateboarding |
|
Task 1: Find the "number" of Total values for the four events in the table:
• n(G7) = the number of Grade 7 Students = 240 (Look under the Totals column.)
• n(G8) = the number of Grade 8 Students = 260 (Look under the Totals column.)
• n(SN) = the number of snowboarding = 270 (Look under the Totals row.)
• n(SK) = the number of skateboards = 230 (Look under the Totals row.)
Task 2: Find the "number" values for specified AND and OR situations from the table:
• n(G7 and SN) = the number of Grade 7 students preferring snowboarding (an intersection of these sets) = 130
• n(G8 and SK) = the number of Grade 8 students preferring skateboarding (an intersection of the sets) = 120
Look to where the TWO events intersect with one another - where the column and row intersect.
• n(G8 or SK) = the number of Grade 8 students or preferences of skateboarding (a union of the sets)
= 260 + 230 - 120 = 370
Look for the total of Grade 8 students + the total of skateboarders, but remember to subtract where these two sets intersect (overlap). In this problem the total number of Grade 8 students choosing skateboarding (120) will appear in the total of "all Grade 8 students" and in the total of "all skateboarders", thus being counted TWICE. Subtracting ONE of the 120's will give the correct total.
Task 3: Find the probability that a person chosen at random will be a Grade 7 students who prefers snowboarding.
This situation is an AND situation (an intersection):
"the person is a Grade 7 student AND the person prefers snowboarding"
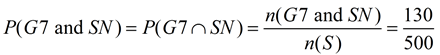
Where n(S) = number in sample space (or the Total of the table).
Task 4: Find the probability that a person chosen at random will be a Grade 8 student or a person who prefers skateboarding.
This situation is an OR situation (a union):
"the person is a female OR the person prefers a sports car"
Two formulas are possible for "OR".
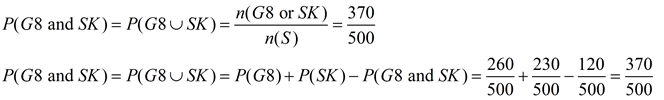
Task 5: Consider a two way relative frequency table.
Two Way Whole Table Relative Frequency
Students |
snowboarding |
skateboarding |
Total |
Grade 7 |
|
|
|
Grade 8 |
|
|
|
Total |
|
|
|
|
You may remember the two way relative frequency table where each entry in the table is divided by a total from the table.
The decimals and fractions seen in this table are giving you the probability of each cell in the table.
(This is a two way "whole table" relative frequency. There are also row and column relative frequency tables.) The decimals may be rounded to two decimal places if needed.
|
These fractions and decimals represent the probability that each cell of the table will occur.
For example, the probability of choosing a Grade 7 student who prefers skateboarding is 110/500 or 22%.
The probability of choosing a Grade 7 student is 240/500 = 48%.
In this table, the concept of "AND" is easily found by finding the intersection of the appropriate row and column.
Unfortunately, this table will not visually yield the probability of more complex situations such those dealing with "OR" situations.
