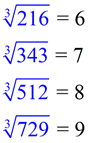|
NOTE: Perfect squares and perfect cubes (in relation to area and volume) is a NGMS standard for Grade 6.
|
|
A square is the result of simply multiplying a number by itself. Any number can be squared.
The verb "to square" denotes this operation.
Example: "to square 9" = 9 x 9 = 81 or 92 = 81 Example: 1.2 x 1.2 = 1.44
" Squaring" is the same as raising to the power of 2, denoted by an exponent of 2.
 An important property of squaring, An important property of squaring,
is that the square of a number is the same as the square of its additive inverse.
The additive inverse of 9 is -9. So,
9 x 9, or (9)2, is the same result as (-9) x (-9), or (-9)2.
Remember, a negative number x a negative number = a positive number.

The term perfect square (or square number) refers to the multiplying of an integer times itself. For example, 4 x 4 = 16,
where 16 is called a perfect square.
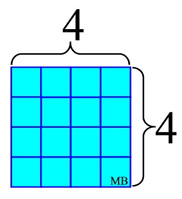
4 "squared" = 16
4 x 4 = 16
written as 42
|
A perfect square number can be visualized as the number obtained by squaring the absolute value of the integer, which then becomes the lengths of the
sides of a square as shown at the left.
Remember, lengths are positive.
The result of this
"squaring" process is the
creation of the value of 16 interior units (the area of the square), which represents the perfect square number.
A list of perfect squares is shown at the right.
You will need to know this list for Grade 8.
|
|
Perfect Squares
0 = 0 x 0
1 = 1 x 1
4 = 2 x 2
9 = 3 x 3
16 = 4 x 4
25 = 5 x 5
36 = 6 x 6
49 = 7 x 7
64 = 8 x 8
81 = 9 x 9
100 = 10 x 10
121 = 11 x 11
144 = 12 x 12
169 = 13 x 13
196 = 14 x 14
225 = 15 x 15 |
|
Yes, a "perfect square" can be the product of a negative integer times itself. Just remember that a negative number times a negative number is a positive number. (-6) x (-6) = 36


A cube is the result of multiplying a number times itself three times. Any number can be cubed.
The verb "to cube" denotes this operation.
Example: "to cube 4" = 4 x 4 x 4 = 64 or 43 = 64 Example: 1.2 x 1.2 x 1.2 = 1.728
" Cubing" is the same as raising to the power of 3, denoted by an exponent of 3.

The term perfect cube refers to the multiplying of an integer times itself three times. For example, 2 x 2 x 2 = 8,
where 8 is called a perfect cube.
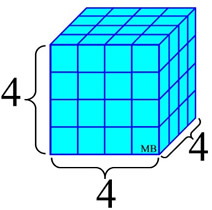
4 "cubed" = 64
4 x 4 x 4 = 64
written as 43
|
A perfect cube number can be visualized as the number obtained by cubing the absolute value of the integer, which then becomes the lengths of the
sides of a cube as shown at the left.
Remember, lengths are positive.
The result of this
"cubing" process is the
creation of the value of 64 interior units (the volume of the cube), which represents the perfect cube number.
|
|
Perfect Cubes
0 = 0 x 0 x 0
1 = 1 x 1 x 1
8 = 2 x 2 x 2
27 = 3 x 3 x 3
64 = 4 x 4 x 4
125 = 5 x 5 x 5
216 = 6 x 6 x 6
343 = 7 x 7 x 7
512 = 8 x 8 x 8
729 = 9 x 9 x 9 |
List of perfect cubes.
You will need to know this list up to 125 for Grade 8. |

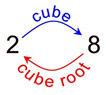
To take the cube root of a number, is to un-do (or reverse) the cubeing process.
Finding the cube root of a number is the inverse operation of cubing the number.
2 cubed = 8
cube root of 8 = 2 |
 |
Cubing: 43 = 64 Cube rooting: 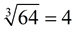
The symbol used for a cube root operations resembles that of as square root, BUT it has the number 3 in the corner of the check mark. You can think of cube rooting as asking the question: "What number times itself three times created the number under the cube root symbol?"
 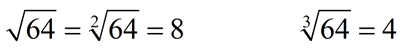
|
|
Notice the small 3 (called the index) in the cube root symbol above.
The symbol for square root can also be written in this style, with a 2 instead of the 3. Since square roots are the most widely used root symbol, the 2 is commonly not shown. So, if there is no small number (the index) indicated, you are dealing with a square root.
There is no issue regarding the placement of a positive or negative sign in front of a cube root symbol (as there was with the square root). When working with cube roots, the sign inside the cube root symbol will determine the sign of the answer.
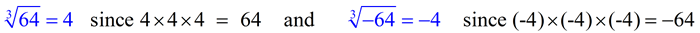
FYI: You will not be working with a negative number under a square root symbol, at this level.
You will study this concept in more advanced courses.
|
|