Fractions are numbers that are used to represent parts of whole quantities.
The denominator of a fraction (the bottom) shows the number of equal parts in the whole.
The numerator of a fraction (the top) shows the number of parts being talked about or being used. 

A pizza arrives from the Deli Shop and it is cut into 8 equally sized pieces. You eat the first piece. It can be said that ... which says that one of the eight total pieces has been eaten.

To compare fractions: a) convert the fractions to a common denominator. The converted fraction with the larger resulting numerator will be the larger fraction. b) convert the fractions to decimal values (divide the top by the bottom) and compare the values.

Properties of Fractions

Given: a, b, c and d are real numbers, variables, or expressions such that b, c, d ≠ 0.

Property:	Example:
1. Signs and Fractions:	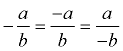The placement of a negative sign can be in front of the fraction, in the numerator or in the denominator.
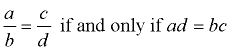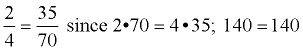
2. Equivalent Fractions:	"Cross Multiply" - In a proportion, the product of the means equals the product of the extremes.
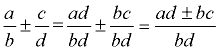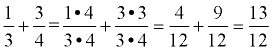
3. Adding & Subtracting:      Get a common denominator.	You can use the product of the two denominators as the common denominator if you cannot find a smaller common denominator.
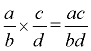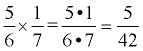
4. Multiplying:	Just multiply through the top and multiply through the bottom.
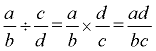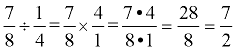
5. Dividing:	Invert (flip) the second term, and multiply.
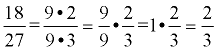
6. Simplify: Search for the largest factor that will divide evenly into both the numerator and denominator. It may be the case that the fraction is already in its simplest form.	Writing all of these steps is not necessary. Just be careful not to make a careless mistake.

You arrive at a party where 4 different pizzas (of the same size) are being served. Since you like all of the pizzas, you decide to assemble one full  pizza by combining parts of each of the available choices. You pick up 1/3 of the cheese pizza, 1/2 of the pepperoni pizza, and 1/8 of the sausage pizza. How much of the anchovy pizza will you need to pick up to complete your "new" whole pizza? Solution:   Let x = fractional part of the anchovy pizza needed to complete the pizza.   Add the portions together and set them equal to 1 (the whole new pizza). Solve for x.      You will only need 1/24 of the anchovy pizza to complete a whole new pizza.  A very small slice!

For help with fractions on your calculator, click here.