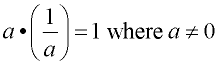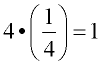|
|
A real number is a value that represents a quantity along a continuous number line. Real numbers can be ordered. The symbol for the set of real numbers is 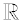 , which is the letter R in the typeface "blackboard bold". |
The real numbers include: counting (natural) numbers ( 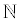 ){1, 2, 3, ... },
whole numbers {0, 1, 2, 3, ... },
integers ( 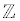 ) {... , -3, -2, -1, 0, 1, 2, 3, ...},
rational numbers ( 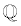 ) (such as -½, 6.25, 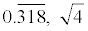 ) ) and
irrational numbers (such as 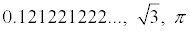 ). |
FYI: The series of three dots ( ... ), seen within the sets above, is called an ellipsis.
As used in mathematics, the ellipsis means "and so forth". |
The properties of the Real Number System will prove useful when working with equations, functions and formulas, as they allow for the creation of equivalent expressions which will often aid in solving problems. In addition, they can be used to help explain or justify solutions.
Chart of Properties
These are the properties you need to know.
|
| |
Property (a, b and c are real numbers, variables or algebraic expressions) |
Examples |
Verbal hints |
1. |
Distributive Property
a • (b + c) = a • b + a • c |
3 • (4 + 5) = 3 • 4 + 3 • 5 |
"multiplication distributes across addition"
|
2. |
Commutative Property of Addition
a + b = b + a |
3 + 4 = 4 + 3 |
"commute = to get up and move to a new location : switch places" |
3. |
Commutative Property of Multiplication
a • b = b • a |
3 • 4 = 4 • 3 |
"commute = to get up and move to a new location: switch places" |
4. |
Associative Property of Addition
a + (b + c) = (a + b) + c |
3 + (4 + 5) = (3 + 4) + 5 |
"regroup - elements do not physically move, they simply group with a new friend." |
5. |
Associative Property of Multiplication
a • (b • c) = (a • b) • c |
3 • (4 • 5) = (3 • 4) • 5 |
"regroup - elements do not physically move, they simply group with a new friend." |
6. |
Additive Identity Property
a + 0 = a |
4 + 0 = 4 |
"the value that returns the input unchanged" |
7. |
Multiplicative Identity Property
a • 1 = a |
4 • 1 = 4 |
"the value that returns the input unchanged" |
8. |
Additive Inverse Property
a + (-a) = 0 |
4 + (-4) = 0 |
"the value that brings you back to the identity element under addition" |
9. |
Multiplicative Inverse Property
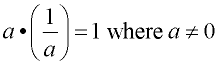
|
|
"the value that brings you back to the identity element under multiplication" |
FYI: Regarding the term "natural numbers", there is no universal agreement about whether to include zero in this set. Most mathematicians hold with the older traditional and define natural numbers to be the counting numbers [positive integers {1, 2, 3, ...}]. Computer scientists, set theorists, logicians and other mathematicians define natural numbers to be the
whole numbers [non-negative integers {0, 1, 2, ...}]. This site will use the term "natural numbers" to refer to the counting numbers {1, 2, 3, ...}.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|