|
When working on a coordinate grid (on graph paper),
there are several ways to find distances (lengths) of line segments.
How to count:
When counting lengths on a coordinate grid, be sure to count the unit lengths (segments). Do not count "boxes".
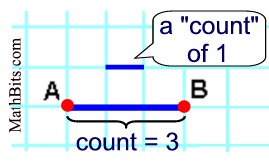
In the diagram at the right, AB = 3 units by counting.
 If the scale on the horizontal axis indicates, for example, that each "horizontal segment" on the grid represents "2 units" (instead of 1 unit), then AB = 6 by counting. |
Count number of "segments" on grid.
This graphic assumes 1 segment = 1 unit. |
Horizontal/Vertical Counting:
This process of "counting" to determine length, works for line segments on the coordinate axes that are vertical or horizontal.
Example 1: Given the graph at the right, find AB and CD.
Solution: Since these segments follow the grids of the coordinate axes, their lengths can be found simply by counting.
AB = 4 units (by counting).
CD = 5 units (by counting).
This method does NOT work for segments placed diagonally across the grid.
|
|
|
|
When line segments are diagonally placed on the coordinate grid, right triangles and the Pythagorean Theorem are needed to find their lengths (or distances).
Example 2: Given the graph at the right, find AB and CD.
Solution: Using the perpendicular nature of the grid lines, you can draw a right triangle with the line segment as its hypotenuse. Count the vertical and horizontal sides of the Δ, and use the Pythagorean Theorem to find the hypotenuse (the slanted segment).
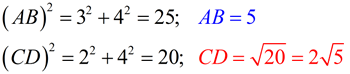(or estimate this answer, such as CD = 4.47)
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
