|
Pythagorean Theorem
c2 = a2 + b2
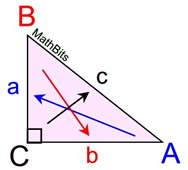
A common method of labeling triangles is shown at the right. When labeling the diagram, a small letter "a" is the length of the side opposite the angle whose vertex is labeled with capital "A". The other sides are labeled in this same manner. |
 |

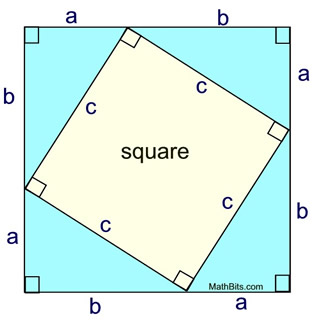
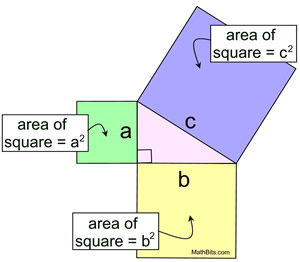
The Pythagorean Theorem can be interpreted in relation to squares drawn to coincide with each of the sides of a right triangle, as shown at the right.
The theorem can be rephrased as, "The (area of the) square described upon the hypotenuse of a right triangle is equal to the sum of the (areas of the) squares described upon the other two sides."
[Remember that the area of a square with a side length of "a" is a × a or a2.]
|
 |

Now, let's see if we can prove (or verify) that these squares (seen above)
are actually connected to one another by the formula a² + b² = c²
(ieor, "area of green square" + "area of yellow square" = "area of purple square").
There are numerous methods for verifying that the Pythagorean Theorem is true.
We will be examining just two of these methods.
Verify the Pythagorean Theorem: |
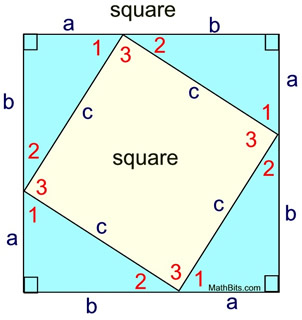
 Square in a Square Approach: Square in a Square Approach:
A blue right triangle, as shown, is copied and arranged in a manner that forms a large square (using its legs) and an inner square (using its hypotenuse).
The four blue triangles are congruent. They each have a right angle and legs of length a and b. (SAS)
We can verify that the inner square is actually a square. We know that in a right triangle, the acute angles add to 90º. m∠1 + m∠2 = 90.
Now, m∠1 + m∠2 + m∠3 = 180 since the three angles for a straight line. Thus m∠3 must be 90º, verifying that the inner quadrilateral is actually a square with 4 right angles. |
|
We are going to take what we now know about the diagram above and see what happens when we rearrange the diagram.
|
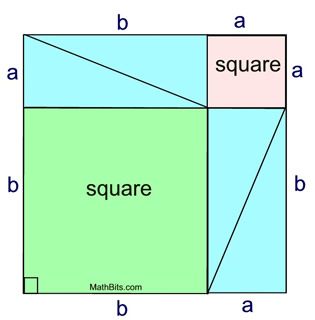
 Rearranging the Diagram: Rearranging the Diagram:
If we re-draw the sub-divisions of the large square seen in the diagram above, we can see the Pythagorean Theorem pop out.
Both squares shown below are the same size, with a side length of a+b. They are each of the same area size.
The eight blue triangles in the diagrams are congruent. They are right triangles with legs of equal lengths. And, all blue triangles have the same area.
|
|
|
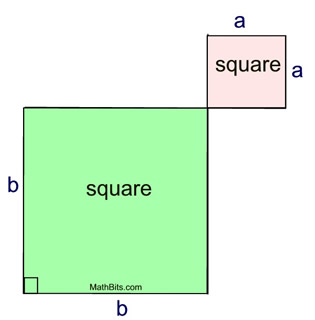
If we remove the four congruent blue triangles from each drawing, the remaining portions will represent equal area. Representing the remaining areas, we see the Pythagorean Theorem. |
|
|
a2 + b2 = c2 |

FYI only: It is also possible to start with our original "square in a square" diagram,
and directly verify the Pythagorean Theorem, with the use of some algebraic skills.
 Algebraic Version: Algebraic Version:
Square in a Square Approach:
A blue right triangle, as shown, is copied and arranged in a manner that forms a large square (using its legs) and an inner square (using its hypotenuse).
The four blue triangles are congruent. They each have a right angle and legs of length a and b. (SAS)
We can verify that the inner square is actually a square. We know that in a right triangle, the acute angles add to 90º. m∠1 + m∠2 = 90.
Now, m∠1 + m∠2 + m∠3 = 180 since the three angles for a straight line. Thus m∠3 must be 90º, verifying that the inner quadrilateral is actually a square with 4 right angles. |
|
Congruent triangles have the same area.
The length of a side of the large square is a + b.
The area of the large square is (a+b) • (a+b).
The area of the inner square is c • c.
The area of a blue triangle is ½ab.
Area of large square = area of inner square + area of the 4 blue right triangles.
(a+b)(a+b) = c • c + 4(½ab)
a2 + 2ab + b2 = c2 + 2ab (now, subtract 2ab from both sides)
a2 + b2 = c2 |

In high school Geometry, you will see that there are both geometrical
and algebraic "proofs" of the Pythagorean Theorem.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|