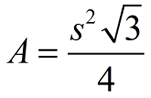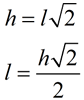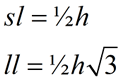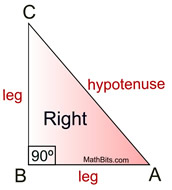
Facts about Right Triangles MathBitsNotebook.com Topical Outline | JrMath Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

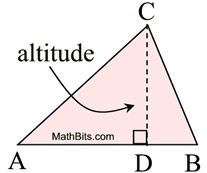
• A right triangle has one right angle.      (A right angle measures exactly 90º.) • A "box" is used to indicate the location of the right angle. • The longest side of the right triangle (across from the "box")      is called the "hypotenuse". • The remaining two sides are referred to as "legs", which may,      or may not, be of equal length.

• Note: It is possible for a right triangle to also be scalene or isosceles.

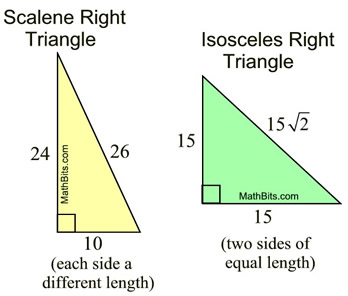
As the diagram above shows, the use of radicals pop up when working with right triangles.
Refer to the Radicals section to review your skills on working with radicals.

• The legs of a right triangle are perpendicular.

• The acute angles of a right triangle are complementary (add to 90º). Example: In the diagram, m∠D = 30º and m∠F = 60º These are complementary ∠s. m∠D + m∠E + m∠F = 180 m∠E = 90 m∠D + 90 + m∠F = 180 m∠D + m∠F = 90 ∠D and ∠F are complementary

Some interesting facts about right triangles:

• Right triangles are used by carpenters, architects, and surveyors to ensure "square corners". Pastures for animals are usually rectangular in shape. A farmer uses a right triangle to check to see if the fencing will form a rectangle. 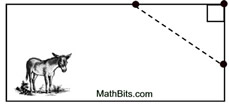Take 3 measurements at a corner and apply the Pythagorean Theorem to be sure you have a right angle in the pasture corner.

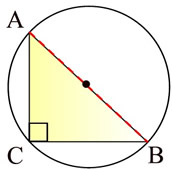
• If a right triangle is inscribed in a circle, the hypotenuse lies on a diameter of the circle. "Inscribed in a circle" means that each vertex of the triangle will lie ON the circle. When a right triangle is inscribed, the hypotenuse will ALWAYS fall on the diameter of the circle.

• All isosceles right triangles are similar. 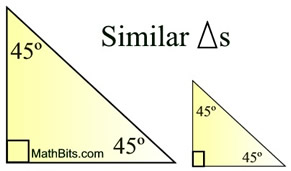The AA method for verifying that triangles are similar is satisfied when comparing all isosceles right triangles.

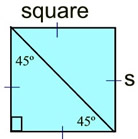
An isosceles right triangle can be viewed as half of a square when the diagonal of the square is drawn. While the area of any triangle is A = ½bh, this formula can be written in a special manner to be used only for isosceles right triangles. (viewed as half the area of a square with side s): 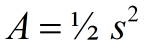The base, b and height, h, can both be expresses as s. A = ½ • s • s = ½ s2

• When the height (altitude) of a triangle is drawn within the triangle, two new right triangles are formed. ΔABC is NOT a right triangle. When altitude is drawn, ΔADC and ΔBDC are right triangles since they each contain a right angle.

• Area of any triangle is A = ½bh. But there is a special area formula for equilateral triangles which uses right triangles. for equilateral triangles only, with side "s" If you are wondering where the radical 3 came from, take a look at the 30º-60º-90º special right triangle mentioned in the section below.    A = ½ • s • ½ s2 = ¼ s2

FYI: "Special right triangles" are two extremely popular right triangles used in mathematics. The features of these triangles make calculations on the triangles easier. There are even special formulas associated with the sides of these triangles.
[The use of the formulas associated with these triangles will appear repeatedly in high school geometry and beyond. The formulas are mentioned here for reference only.]

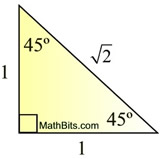
• Special Right Triangle 45º - 45º- 90º • (angles) ratio 1:1:2 • (sides) ratio 1:1: Formulas: Let l = leg h = hypotenuse This is an isosceles right triangle.

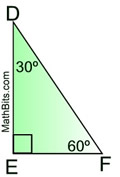
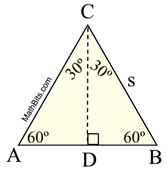
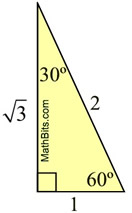
• Special Right Triangle 30º - 60º - 90º • (angles) ratio 1:2:3 • (sides) ratio 1:2: Formulas: Let sl = short leg    (opposite 30º ∠) ll = long leg    (opposite 60º ∠) h = hypotenuse