|
A quick review of transformations in the coordinate plane.
Remember that a reflection is simply a flip. Under a reflection, the figure does not change size (it
is a rigid transformation).
It is simply flipped over the line of
reflection.
The orientation (lettering of
the diagram) is reversed.
|
line reflection in x-axis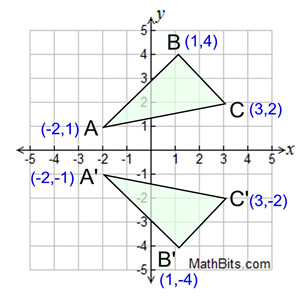
|
Reflection
in the x-axis: |
When you reflect a
point across the x-axis, the x-coordinate remains the
same, but the y-coordinate is transformed into its opposite.
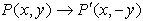 or
or 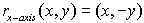
|
Reflection
in the y-axis: |
When you reflect a
point across the y-axis, the y-coordinate remains the
same, but the x-coordinate is transformed into its opposite.
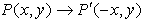 or
or 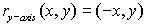
|
Reflection
in y = x: |
When you reflect a
point across the line y = x, the x-coordinate
and the y-coordinate change places.
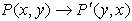
or 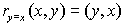 |
Reflection
in y = -x: |
When you reflect a
point across the line y = - x, the x-coordinate
and the y-coordinate change places and are negated (the signs
are changed).
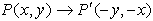
or 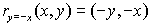 |

A point reflection exists when a figure is
built around a single point called the center of the
figure.
For every
point in the figure, there is another point found directly opposite it on
the
other side of the center.
The figure does not change size (it is
a rigid transformation).
|
point reflection in origin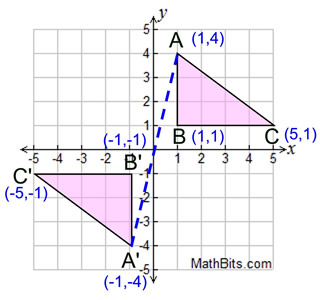
|
Reflection in the Origin: |
While any point in the
coordinate plane may be used as a point of reflection, the most
commonly used point is the origin.
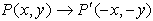 or
or 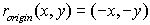
|

A rotation turns a figure through an angle about a fixed point called the center.
The most popular center of rotation is the origin, but may be other points.
A positive angle of rotation turns the figure counterclockwise, and a negative angle of rotation turns the figure
in a clockwise direction.
The figure does
not change size (it is a rigid transformation).
|
rotation 90º counterclockwise centered at origin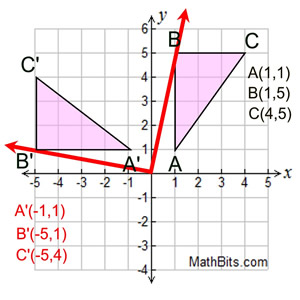
|
Rotations on the coordinate axes are assumed to be counterclockwise (CCW),
unless otherwise stated.
Rotation of 90º: (CCW) |
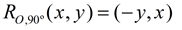 |
Rotation of 180º: (CCW) |
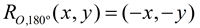 (same as reflection in origin)
(same as reflection in origin) |
Rotation of 270º: (CCW) |
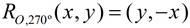 |
If a problem specifically asks for a clockwise (CW) rotation on the axes,
the formulas stated above for 90º and 270º will not work.
Instead, you will need: (for clockwise only) 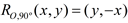 and and 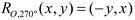 . .
The formula for a rotation of 180º is the same in both directions. 
A dilation is a
transformation that produces an image that is the same shape as the
original, but is a different size (the figures are similar).
The description of a dilation includes the scale factor and the center of the
dilation.
A dilation "enlarges" or "reduces" a figure
(it is not a rigid transformation).
|
dilation of scale factor 2 centered at the origin.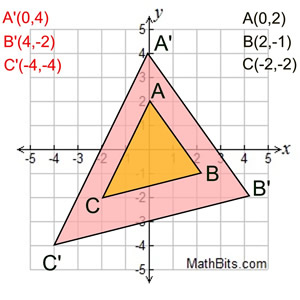 |
Dilation of scale factor k: |
The center of a
dilation is most often the origin, O. It may however, be some other point in the coordinate plane which will be specified.
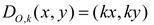 |

A translation "slides" an object a fixed
distance in a given direction.
The original object and its translation have the same shape and size (it is a rigid transformation), and they face in the same direction.
|
translation 6 units left and 3 units up.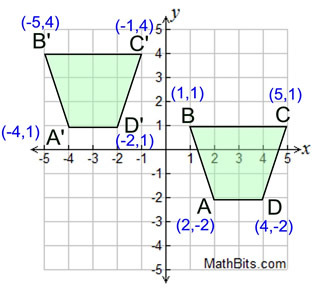 |
Translation of h, k: |
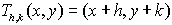
If h > 0, the original object is shifted h units to the
right.
If h < 0, the original object is shifted | h | units to the left.
If k > 0, the original object is shifted k units up.
If k < 0, the original object is shifted | k | units down. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|





