|
Let's quickly review what we already know about rotations
and how the pre-image and image are positioned in relation to one another.
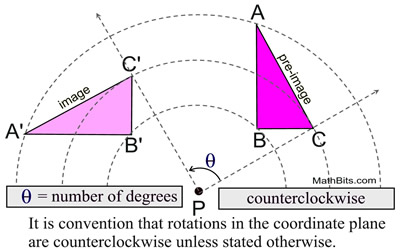
 An object and its rotation about a point maintain the same shape and size. They are rigid transformations. An object and its rotation about a point maintain the same shape and size. They are rigid transformations.
During a rotation, points making up the rotated figure will always retain their same distances from the point of rotation.
In a rotation, points follow arc "paths" that enable them to always be the same distance from the point of reflection. Notice the arc "paths" in the diagram at the right.
|
 If you need additional information on rotations,
If you need additional information on rotations,
go to the section on Transformations.
|
While the degree of rotation can theoretically be any numerical value, certain limitations are placed upon formal constructions (with compass and straightedge) when creating degrees of rotation.
Typically, angles such as 30º, 45º, 60º, 90º, 180º, and 270º are examples of constructed angles. These angles often have an association with a perpendicular construction, and/or the bisecting of a previously constructed angle. See Construct Angles of Specific Size to see more about formal angle constructions. |
 Constructing a rotation of 180º can be seen at Construct: Reflection in a Point. Constructing a rotation of 180º can be seen at Construct: Reflection in a Point.
Remember, a reflection in a point is the same as a rotation of 180º about the point. |

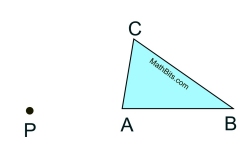
 Rotation of 90º CCW about a point. Rotation of 90º CCW about a point.
Given: ΔABC and point P, the center of the rotation.
Task: Construct a 90º counterclockwise rotation of ΔABC about point P and label it ΔA'B'C'
|
|
Remember, that in a rotation, points A, B and C will always remain their same distances from point P.
Remember, also, that 90º is associated with perpendicular lines.
|
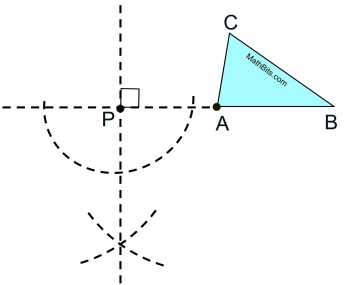 |
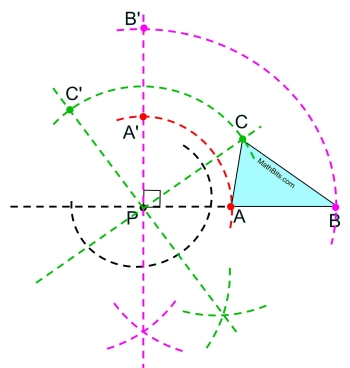
Let's start this construction
by rotating point A.
Draw a line starting at A and extending through P. Draw beyond P to the left.
A perpendicular at P will establish the 90º relationship needed.
Construct a line perpendicular to the line at point P.
(You know this construction.) |
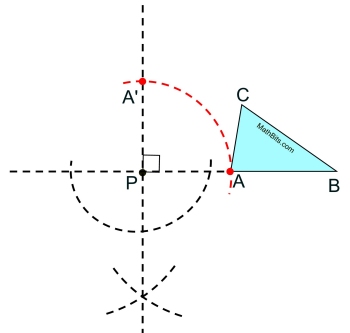 |
Put your compass point at P, measure to point A and make the arc path of point A to the left (counterclockwise).
Where the arc intersects with the perpendicular line will be the image of A.
The distance from P to A is the distance from P to A' (a 90º rotation). The radii are congruent.
We have the rotation of point A
labeled A'.
|
 |
What about the other two vertices
of the triangle?
At this point, this process needs to be repeated for points B and C.
• Draw a line to connect point P to C.
• Extend the line to the left of P.
• Construct a perpendicular through P to the "new" line.
• Measure distance from P to C onto the perpendicular line.
• THEN, repeat again for point B.
• Draw ΔA'B'C' to complete this construction.
Note: In this construction, one side of the triangle is horizontal. The same perpendicular used for point A will also be used for point B. |
But a shorter method is possible by examining the lengths of the remaining sides of the triangle in relation to point A and their arc paths. |
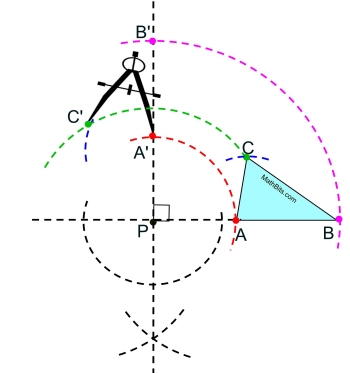 |
As the rotation occurs, the distances between the vertices of the triangle will remain constant. Rotation is a rigid transformation.
After constructing the location of A',
• Draw the arc paths for points B and C from point P.
• Measure the distance from A to C on the triangle.
• Mark off that distance, starting from A' and intersecting with the "path" of point C.
Remember this constuction is CCW (counterclockwise).
• This is now the length from point A' to point C'.
|
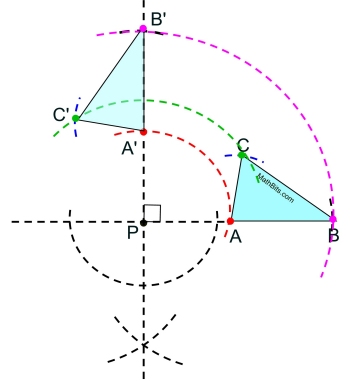 |
Repeat this process to locate B'.
• Measure the distance from A to B on the triangle.
• Mark off that distance, starting from A' and intersecting with the "path" of point B.
• This is point B'.
Draw ΔA'B'C'. |

Let's take a glimpse at some simple rotations about some more difficult angles.
Rotate point A 45º CCW about point P.
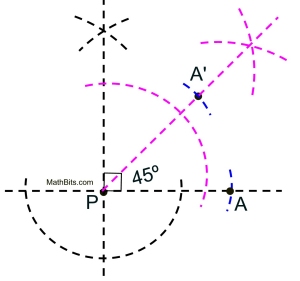 |
The is no specific construction for 45º.
But we know that 45º is half of 90º, and we know how to construct 90º (construct a perpendicular).
We also know how to bisect an angle, which cuts the angle into two equal sizes.
Since 90 º = ½ (45º), bisect will do nicely.
• Construct a perpendicular at point P.
• Bisect the right angle formed in the upper right section from the perpendicular.
• Copy length PA onto the ray through P to A'.
• DONE. |
Rotate point B 60º CCW about point P.
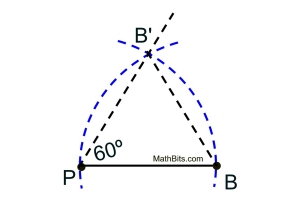
Segments showing the "triangle"
are not required. |
The is no specific construction for 60º.
But we know that an equilateral triangle contains 60º angles, and we know how to construct that triangle.
• Draw a segment connecting P to B.
This will be a side of the equilateral triangle.
• Copy length PB, making an arc above the segment from point P, and then from point B.
• Draw a line connecting P to B' to form a 60º angle.
• Since the arcs had length PB, no further measurements are needed.
• DONE. |
| Rotate point C 135º CW about point P.
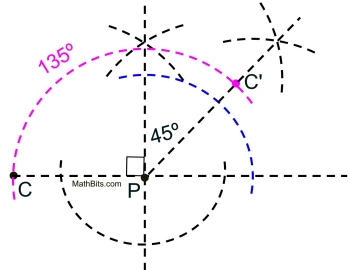
The large pink arc, from C to C', shows the 135º angle. This "large" arc is not required. Small arcs at C and at C' would show "copy length PC".
|
The is no specific construction for 135º.
But we know that 90º + 45º = 135º. We will need to construct 90º (construct a perpendicular), and then bisect one section to create the additional 45º.
Keep in mind that this is an obtuse angle and what it will look like in relation to point P.
• Construct a perpendicular at point P.
• Bisect the right angle formed in the upper right section from the perpendicular to get 45º.
• Copy length PC onto ray through P to C'.
• DONE.
Since this construction was CW (clockwise), we were moving to the right in rotating point C. |
Rotate point D 240º CCW about point P.
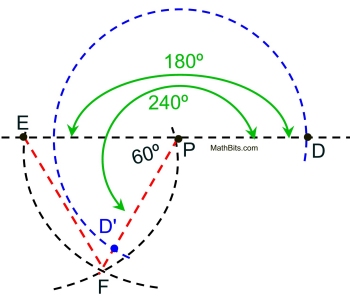
The solid green arcs are NOT part of the construction. They are simply showing you where the 180º line is located, and where the final construction of 240º is complete. The large blue arc path could be two small arcs at D and D'. |
The is no specific construction for 240º.
But we know that 180º + 60º = 240º. We will need to draw a straight line (180º) and then construct an equilateral triangle for the 60º.
Keep in mind that this is a reflex angle (greater than 180º) and what it will look like in relation to point P.
Also, this rotation is CCW, so point D is moving to the left.
• Draw a straight line through D and P.
• Construct an equilateral triangle.
(You know this construction).
• Designate EP as length of a side of the Δ.
• Construct arc length EP from E and P to get point F, forming equilateral ΔPEF.
• Draw segment from E to P.
• DONE. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|