|
Cones are three-dimensional closed surfaces.
They are not polyhedra since their faces are curved surfaces, not polygons.
 |
In many ways, however, a cone is similar to a pyramid.
A cone's base is simply a circle rather than a polygon as seen in the pyramid.
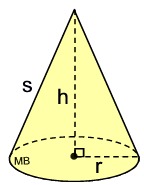
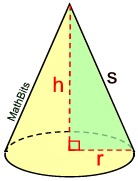
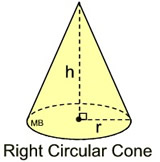
r = radius; h = height; s = slant height
It is possible that the base of a cone may be another curved surface, such as an oval, but for this level course, the base will be a circle.
|
|
A cone is a three-dimensional closed figure that has a circular base connected to a vertex (or apex) point outside the plane of the base. |
|
Right Circular Cone |
Regarding circular cones:
• |
The one and only base of the cone is a circle |
• |
The vertex of a cone (the point, the apex) is not in the same plane as the base. |
• |
While cylinders have several characteristics in common with pyramids, they are not pyramids. |
• |
A cone sitting straight up and down is called a right circular cone.
|
|
The word "cone" usually refers to a cone whose base is a circle, resembling the cone in an ice cream cone. An ice cream cone is a right circular cone, with its base at the top.
It may be the case that a cone is "slanted", called oblique.
At this level, we will concentrate on cones that are straight up and down.
|
 |
 |
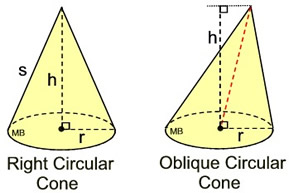If the segments joining the center of the circle base and vertex point is perpendicular to the base, the cone is a right circular cone. If the segment joining the center of the circle base and vertex point in not perpendicular to the base, the cone is called an oblique circular cone.
h = height; r = radius; s = slant height
|
Cross Sections (Plane Sections) of Right Circular Cones |
Parallel to Base
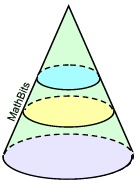All slices made parallel to the base create "circles" that are similar to the base (same shape but not necessarily the same size). |
Perpendicular to Base
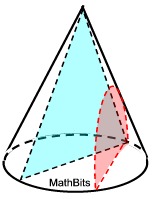A slice through the vertex (top, apex) perpendicular to the base (at its center) will be a triangle. Any other slices perpendicular to the base (not through the top) will be part of an arc shape called a hyperbola. |
Slice Orientation Slanted
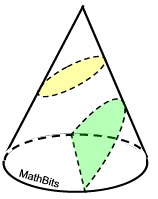Slices that are not parallel nor perpendicular to the base will create cross sections that are ovals (ellipses) and part of an arc shape called a parabola. |
|
The volume of a cone is one-third the area of its base times its height.
 |
|
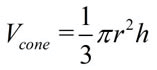The volume of a cone can be calculated in the same manner as the volume of a pyramid:
the volume is one-third the product of the base area, πr2, times the height of the cone.
|
Since the base of a cone is a circle, you can see how replacing the B value in the volume of the pyramid with the area of a circle gives us the volume formula for a cone.
 |
|
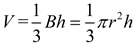V = volume in cubic units
r = radius of base in units
h = height in units
|
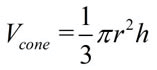
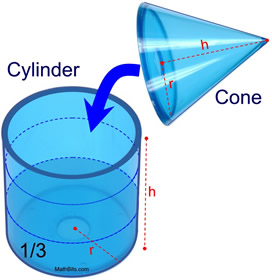
Also notice that the volume of a cone is one-third the volume of a cylinder with the same base and height.
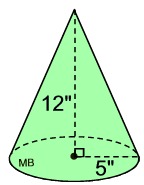
Example:
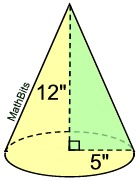
Find the volume of this right circular cone, to the nearest tenth of a cubic inch.
Solution:
• The radius = 5 inches.
• The height = 12 inches.
• The volume formula is:
 |
|
|
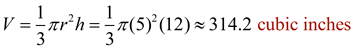Justification of formula by "pour and measure":
(For this discussion, our cone will be a right circular cone.)
We can conduct an experiment to demonstrate that the volume of a cone is actually equal to one-third the volume of a cylinder with the same base and height. We will fill a right circular cone with water. When the water is poured into a cylinder with the same base and height as the cone, the water fills one-third of the cylinder.
| • |
The base of the cone is a circle, with an area π r2. |
| • |
The base of the cylinder is also a circle with an area of π r2. |
| • |
The height of the cone and the cylinder is h. |
| • |
The volume of the cylinder is V = π r2 h. |
| • |
Since the water from the cone fills one-third of the cylinder, the volume of the cone is one-third the volume of the cylinder:
|
|
|
By measurement, it can be concluded that the height (depth) of the water in the cylinder is one-third the height of the cylinder. Since the formula for the volume of the cylinder is V = π r2h, it follows that the volume of the cone can be represented by  .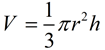
Surface Area of a Cone:
|
The surface area of a closed right cone is a combination of the lateral area and the area of the base. |
|
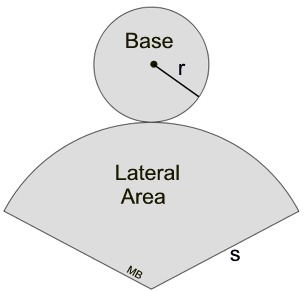
When cut along the slant side and laid flat, the surface of a cone becomes one circular base and the "sector" of a circle (lateral surface), as seen in the net at the right.
A sector is "part" of the interior of an entire circle. The sector in this net looks like a very large piece of pizza (more than a quarter of an entire pizza). The radius of the pizza will be "s". The "s" is actually the slant height of the cone, and "r" is the radius of the base of the cone.
The length of the arc of this sector (the curved edge) is the same as the circumference of the small circular base. |
|
Total Surface Area of a Closed Cone
SA = sπr + πr2
SA = surface area
r = radius of the base
s = slant height of the cone |
In a right circular cone, the slant height, s, can be found using the Pythagorean Theorem.
Create a right triangle using the height, the radius and the slant height.
s2 = r2 + h2
 |
 |
|
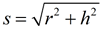When asked to find the surface area of a cone,
be sure to read the question carefully.
|
Will the surface area
include the base?
SA = sπr + πr2
|
Will the surface area
NOT include the base?
SA = sπrh |
Example:
Find the surface area of this right circular cone with a closed base. Express answer in terms of pi.
Solution:
• We need to know the slant height, s. Use the Pythagorean Theorem in the triangle, s2 = 122 + 52.
s2 = 144 + 25 = 169; s = 13
• The volume formula is SA = sπr + πr2
SA = 13•π•5 + π(5)2 = 65π + 25π = 90π square inches |
|
|
|
A frustum is a portion of a solid (usually a pyramid or a cone) which remains after its upper part has been cut off by a plane parallel to its base. |
|
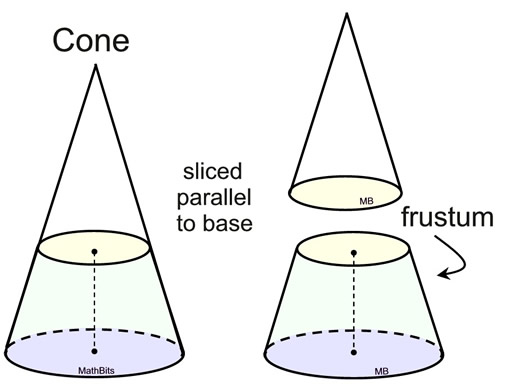
To find the volume of a frustum,
find the volume of the entire large cone
and subtract the volume of the smaller cone being cut off of the top.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
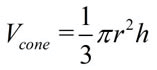
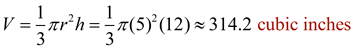
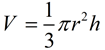