Note: Actual dimensions used on this page may be rounded to the nearest tenth of a unit.
We found the surface area of the polyhedra on this page. Now, we will find their volumes.
These polyhedra are composed of polygons beyond triangles and quadrilaterals.
Remember: Volume is labeled in " cubic units".
Remember: "Regular" means a polygon has all of its sides of equal measure,
and all of its angles of equal measure.

|
V = Bh
V = volume, B = area of the base, h = height of the solid |
 Right Regular Pentagonal Prism |
|
|
1. Find the volume
of this right regular pentagonal prism.•
Solution:
Area of triangles in base of regular pentagon:
A = 5•
(½ bh) =
5•
(½(8)(11)) = 220 sq. in.
• Volume using B = 220 and h = 18
V = Bh = 220 • 18 = 3960 cubic inches
|
|

 Right Regular Octagonal Prism |
|
| 2. Find the volume of this right
regular octagonal prism.
Solution:
• Area of triangles in base of regular octagon:
A = 8•
(½ bh) =
8•
(½)(6.8)(8.2) = 223.04
• Volume using B = 223.04 and h = 20.2
V = Bh = 223.04 • 20.2 = 4505.408 cubic units |
|

 Right Irregular Pentagonal Prism |
|
3. Find the volume
of this right
irregular pentagonal prism.
Solution:
• Area of trapezoid part of base:
(decompose) A = 6 + 27 + 6 = 39 sq.in.
(formula) A =
½ h (b1 + b2) = ½ 3 (9 + 17) = 39 sq.in.
• Area of triangle part of base:
A = ½ (17)(8) = 68 sq.in.
Total area of base: 39 + 68 = 107 sq. in.
• Volume using B = 107 and h = 15
V = Bh = 107 • 15 = `1605 cubic inches
|
|

In the first two examples, we used triangles drawn from the center of the regular polygons to find the apothem of the polygon and the area of the triangle. This strategy allowed us to find the area of the bases of the solids quickly and easily.
This method WILL NOT WORK with irregular polygons. Irregular polygons do not have a "center" that is equidistant from the polygon's sides (an apothem). They do have a "center of balance" (a geometric center or "centroid"), but this location is not equidistant from the sides.
You will learn more about the centroid of a polygon in later courses.

|
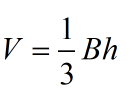
|
V = volume, B = area of the base,
h = height of the solid |
 Right Regular Hexagonal Pyramid
|
|
|
4. Find the volume
of this
right regular hexagonal pyramid.
The height of the pyramid is 35 units.
Solution:
• Area of base regular hexagon:
ABase = 6(½(10)(8.7)) = 261
• Volume using B = 261 and h = 35
V = (1/3)Bh = (1/3) • 261 • 35 = 3045 cubic units
|
|

 Right Irregular Pentagonal Pyramid |
|
|
5. Find the volume
of this
irregular right pentagonal pyramid. The height of the pyramid is 10 units.
Solution:
• Find the area of the composite base:
Area of square =36, and area of triangle
=½ (6)(2)=6, for a total area of 42 sq. units.
• Volume using B = 42 and h = 10
V = (1/3)Bh = (1/3) • 42 • 10 = 140 cubic units
|
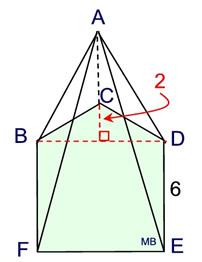
The "2" is the height of Δ BCD.
|